


![[f(g(x))]' = f'(g(x)) \cdot g'(x) [f(g(x))]' = f'(g(x)) \cdot g'(x)](/latexrender/pictures/1cf29622b56763ffe25ee73d877042d8.png) , então
, então ![f(g(x)) = \int [f(g(x))]' \, dx = \int f'(g(x)) \cdot g'(x) \, dx f(g(x)) = \int [f(g(x))]' \, dx = \int f'(g(x)) \cdot g'(x) \, dx](/latexrender/pictures/004eb49c2c294a6f59c553dfc6add141.png) . Se você tivesse
. Se você tivesse ![[f(g(h(x)))]' [f(g(h(x)))]'](/latexrender/pictures/bcd8f23899892aa9864673705bed71d4.png) , apenas teria que fazer substituição duas vezes ao invés de uma.
, apenas teria que fazer substituição duas vezes ao invés de uma.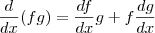 , daí
, daí  . Integrando, temos
. Integrando, temos 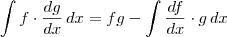 .
. , pois isto não é válido para diferenciais. É um assunto um pouco mais avançado que deve ser tratado com cautela.
, pois isto não é válido para diferenciais. É um assunto um pouco mais avançado que deve ser tratado com cautela.

Jhenrique escreveu:E nesta imagem abaixo, o profº Luiz Aquino derivada a expressão u = x implicando em du = dx.
(...)

MarceloFantini escreveu:O método de substituição é feito justamente para voltar à regra da cadeia: se, então
![f(g(x)) = \int [f(g(x))]' \, dx = f(g(x)) = \int [f(g(x))]' \, dx =](/latexrender/pictures/f3f78c64d0b2ea5d3c20f6e031938478.png) . Se você tivesse
. Se você tivesse, apenas teria que fazer substituição duas vezes ao invés de uma.

MarceloFantini escreveu:Sobre a integral por partes ser definida pela regra do quociente, note que a regra do quociente pode ser deduzida a partir da regra do produto, então é mais prático pelo produto.
MarceloFantini escreveu:A dedução da integração por partes é como segue: temos, daí
. Integrando, temos
.
MarceloFantini escreveu:Sobre a notação, se as duas funções são iguais então seus diferenciais são iguais, mas não é verdade que d^2 u = dx^2, pois isto não é válido para diferenciais. É um assunto um pouco mais avançado que deve ser tratado com cautela.

essa demonstração que vc fez, que eu tbm já havia imaginado, não coincide com a fórmula de integração por substituição...
[f(x) : g(x)]' = [f(x) · g?¹(x)]'
não me parece uma boa ideia.
 , e não
, e não 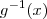 que denota a função inversa. Para a dedução, observe que
que denota a função inversa. Para a dedução, observe que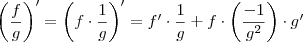
 .
.Continuo sem entender a ideia do porque proceder assim... vc integrou a 2ª igualdade e ñ a 1ª, não entendi o pq... na regra da cadeia a ideia é fazer o diferencial do denominador ser igual ao do numerador e assim sucessivamente... e na integração, qual é a jogada?
acho explicação sobre isso em livros de cálculo?


MarceloFantini escreveu:Qual é a "fórmula" de integração por substituição que você conhece?
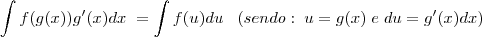
MarceloFantini escreveu:Aprenda a usar a notação. O correto é, e não
que denota a função inversa.
MarceloFantini escreveu:Sobre a integral por partes ser definida pela regra do quociente, note que a regra do quociente pode ser deduzida a partir da regra do produto, então é mais prático pelo produto.
MarceloFantini escreveu:Para a dedução, observe que.


Continuo sem entender a ideia do porque proceder assim... vc integrou a 2ª igualdade e ñ a 1ª, não entendi o pq... na regra da cadeia a ideia é fazer o diferencial do denominador ser igual ao do numerador e assim sucessivamente... e na integração, qual é a jogada?
MarceloFantini escreveu:Não sei o que quer dizer sobre o diferencial do denominador ser igual ao do numerador, não faz sentido para mim. Pode ilustrar com um exemplo?

MarceloFantini escreveu:acho explicação sobre isso em livros de cálculo?
Não. Se encontrar, será no livro de Cálculo do Richard Courant, Introduction to Calculus and Analysis.

(Mudança de variável). Sejamcontínua,
derivável, com
integrável e
. Então
.
Certo, matemáticamente está errado. Agora, como faço pra expressar verbalmente que uma função inversa é diferente duma função inversa?
![\frac{1}{f(x)} = [f(x)]^{-1} \frac{1}{f(x)} = [f(x)]^{-1}](/latexrender/pictures/324c50023b80bf5a18cd17094a198cc0.png) , é diferente da função inversa,
, é diferente da função inversa,  .
.Você está me dizendo que se caso eu precisar integrar a função abaixo:
facilita se eu fizer assim?
Se eu não estiver errado... é uma sequência lógica que pode ser escrita linearmente... parece haver uma jogada muita semelhante na regra da cadeia inversa (integração por substituição) que eu ainda não captei...
 .
.But, my english is very trash! iahiaheiah
É perdir demais se eu pedisse pra vc me explicar?


MarceloFantini escreveu:Vou referenciar o teorema usado no livro "Um Curso de Análise, Volume 1" pelo autor Elon Lages Lima:(Mudança de variável). Sejamcontínua,
derivável, com
integrável e
. Então
.
MarceloFantini escreveu:O método de substituição é feito justamente para voltar à regra da cadeia: se, então
.
MarceloFantini escreveu:O inverso da função,, é diferente da função inversa,
.
 .....
..... 
MarceloFantini escreveu:
Se eu não estiver errado... é uma sequência lógica que pode ser escrita linearmente... parece haver uma jogada muita semelhante na regra da cadeia inversa (integração por substituição) que eu ainda não captei...
Na notação de Leibniz isto apenas serve para dar a impressão de que os diferenciais "cancelam-se". Mesmo com este exemplo, não vejo onde está a idéia que você disse, de que o diferencial do numerador é igual ao diferencial do denominador.
MarceloFantini escreveu:Se você prefere, integração por substituição poderia ser escrita assim:.
 ..... Bacana!
..... Bacana!

MarceloFantini escreveu:Sim, pois eu também não domino o assunto, estou ainda um pouco longe disso. Um outro conselho: se pretende estudar alguma coisa além de cálculo, suas chances de obter tal conhecimento são bem pequenas na literatura em português.

Perdoe-me pela falta de clareza... eu quis dizer que, na notação de Leibniz, o diferencial do denominador duma "fração" é o mesmo diferencial do numerador da "fração" seguinte...
 ), pois ela é mais facilmente estendida.
), pois ela é mais facilmente estendida.Mas novamente sua dedução não coincide com a definição, pois ela é
enquanto que a sua conclusão é
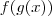 para
para  na primeira integral e
na primeira integral e 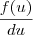 para
para 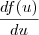 na segunda.
na segunda.Duas perguntas:
1ª Então esse minha pergunta é pertinente a qual tópico da matemática?
2ª O que é estudado depois do cálculo?


MarceloFantini escreveu:Só porque deduzi de maneira diferente não quer dizer que está errada, além disso é um teorema e não uma definição.
MarceloFantini escreveu:Corrigi alguns erros de notação, basicamente depara
na primeira integral e
para
na segunda.
MarceloFantini escreveu:Novamente, não é uma definição e sim um teorema. Se você olhar novamente verá que coincide, note que eu apenas não coloquei os limites de integração e fui mais heurístico, sem enunciar tantas hipóteses, uma discussão mais intuitiva. Se continua achando que não coincide, aponte por favor as diferenças (não apenas de notação, mas conceitualmente, caso contrário não são relevantes).
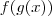 é uma função derivada
é uma função derivada  ... senão não é regra da cadeia! :S
... senão não é regra da cadeia! :S
Não disse que você está errado, disse que a sua demonstração não coincide com a da definição (definição num sentido canônico). Até porque meu modo de pensar é igual ao seu.
O erro na segunda integral foi meu, perdoe-me. Quanto ao erro na primeira, foi seu.
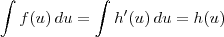 , para que possamos chegar a uma primitiva explícita, o que não necessariamente acontece. Ou seja, minha notação não está errada, eu apenas estou mostrando como se integra uma regra da cadeia e como integração por substituição é uma tentativa de transformar uma função numa regra da cadeia para que se possa integrar mais facilmente.
, para que possamos chegar a uma primitiva explícita, o que não necessariamente acontece. Ou seja, minha notação não está errada, eu apenas estou mostrando como se integra uma regra da cadeia e como integração por substituição é uma tentativa de transformar uma função numa regra da cadeia para que se possa integrar mais facilmente.

MarceloFantini escreveu:Não errei. O que acontece é que no teorema e como escrevi anteriormente não queremos dar a impressão de que a função já será uma primitiva. Minha notação para a regra da cadeia não está errada, nem meus passos seguintes. O ponto é que a idéia é que, para que possamos chegar a uma primitiva explícita, o que não necessariamente acontece. Ou seja, minha notação não está errada, eu apenas estou mostrando como se integra uma regra da cadeia e como integração por substituição é uma tentativa de transformar uma função numa regra da cadeia para que se possa integrar mais facilmente.




Jhenrique escreveu:Se você afirma que o teorema é como o corrigido por você, então, essa demonstração abaixo que o Luiz faz não está certa?
[http://www.youtube.com/playlist?list=PLFAD938CE631F6449][aula 28]
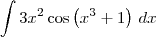
 e
e 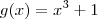 . Note que dessa maneira temos
. Note que dessa maneira temos  e
e  .
.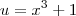 . Teremos então que
. Teremos então que  . Desse modo, podemos escrever que:
. Desse modo, podemos escrever que: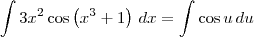
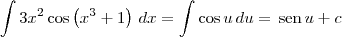
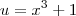 . Sendo assim, podemos dizer no final que:
. Sendo assim, podemos dizer no final que:

 . Calcule a derivada dessa função e verifique que ela coincide com o que está no integrando.
. Calcule a derivada dessa função e verifique que ela coincide com o que está no integrando.
fabriel escreveu:Grande LCMAquino.






Jhenrique escreveu:Eu não entendo a análise dimensional que você, e outras publicações de cálculo fazem, para chegar a conclusão de que tudo isso é a mesma coisa! :S
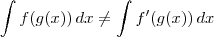 .
.

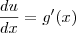 ? Vale lembrar que aqui, por conveniência, estamos usando duas notações diferentes para indicar as derivadas: a notação de Leibiniz (para a derivada de u) e a notação de Lagrange (para a derivada de g).
? Vale lembrar que aqui, por conveniência, estamos usando duas notações diferentes para indicar as derivadas: a notação de Leibiniz (para a derivada de u) e a notação de Lagrange (para a derivada de g).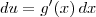 ?
?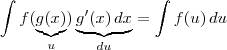



Jhenrique escreveu:Então se a relação abixo é verdadeira...
O que não está claro pra mim é: porque vc usa a (i) dedução em cálculo se a integração por substituição é baseada na regra da cadeia e esta é justamente aplicada na (ii) dedução.
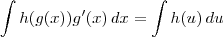


Jhenrique escreveu:Então, para fechar o assunto... aplicando (i) e (ii) numa mesma função e comparando os resultados obtidos, eles serão os mesmos! Certo?
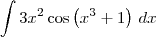
 e
e 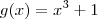 e aplicamos o formato (i).
e aplicamos o formato (i). e
e 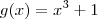 e aplicaremos o formato (ii). Mas atenção: não confunda o f' do formato (ii) achando que seria a derivada da f do formato (i)!
e aplicaremos o formato (ii). Mas atenção: não confunda o f' do formato (ii) achando que seria a derivada da f do formato (i)!
 , então temos que
, então temos que  .
.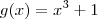 , então temos que
, então temos que 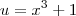 e
e  .
. e
e 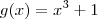 , temos que
, temos que 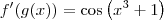 .
.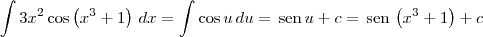

ibiel bad escreveu:alguem pode me ajudar com meus exercicios de funçao por favor ? tenho prova amanha pff afs

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.