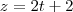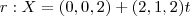por iarapassos » Ter Set 18, 2012 23:24
por iarapassos » Ter Set 18, 2012 23:24
Determine a equação da superfície esférica definida pelas seguintes condições:
centro na interseção de
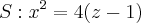
com o eixo
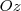
e é tangente a reta

.
Não sei como determinar a interseção entre superfície e o eixo
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por young_jedi » Qua Set 19, 2012 11:00
por young_jedi » Qua Set 19, 2012 11:00
veja amigo que qualquer ponto sobre o eixo z tem coordenadas do tipo

logo substituindo na equação do plano

encontrando z voce tera a intersecção entre o eixo e o plano
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por iarapassos » Qua Set 19, 2012 16:30
por iarapassos » Qua Set 19, 2012 16:30
Obrigada!
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por iarapassos » Sex Set 21, 2012 17:04
por iarapassos » Sex Set 21, 2012 17:04
e agora para achar a equação da superfície.
eu pensei o seguinte:
Como a reta é tangente a S, então eu faria a d(C,r) e encontraria o valor do raio. Porém preciso de um ponto de r, para fazer esse cálculo.
Transformando a equação de r, numa equação vetorial, tenho que r: X=(0,0,1)+t(2,1,1).
A distancia de r a C é dada por
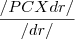
, sendo P um ponto de r, porém PC será um vetor nulo, uma vez que tem as mesmas coordenadas.
Sendo assim, como resolver esse problema?
Há outra forma?
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por young_jedi » Sex Set 21, 2012 18:17
por young_jedi » Sex Set 21, 2012 18:17
repare que quando vc parametrizou r voce cometeu um pequeno equivoco
se voce diz que y=t
então

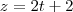
portanto
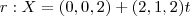
escolha um ponto P que pertença a reta e encontre PC e utilize a relação que vc colocou de produto vetorial para encontrar a distancia de C a r.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Superfície Esférica
por iarapassos » Sex Set 21, 2012 17:24
- 1 Respostas
- 1540 Exibições
- Última mensagem por young_jedi

Sex Set 21, 2012 18:30
Geometria Analítica
-
- [Superficie Esférica]
por EloiCamara » Ter Jan 10, 2017 12:44
- 1 Respostas
- 1861 Exibições
- Última mensagem por adauto martins

Qui Jan 12, 2017 14:46
Geometria Analítica
-
- [SUPERFICIE] Esférica. num tetraedro
por amigao » Sáb Jun 29, 2013 22:39
- 1 Respostas
- 1573 Exibições
- Última mensagem por young_jedi

Dom Jun 30, 2013 14:34
Geometria Analítica
-
- [SUPERFICIE] Posição relativa de reta em uma sup esférica
por amigao » Sáb Jun 29, 2013 11:23
- 1 Respostas
- 2085 Exibições
- Última mensagem por young_jedi

Dom Jun 30, 2013 18:04
Geometria Analítica
-
- COORDENADAS ESFÉRICA
por ALEXSANDRO » Qua Jun 06, 2012 02:56
- 3 Respostas
- 2030 Exibições
- Última mensagem por LuizAquino

Qua Jun 06, 2012 19:44
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
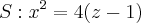 com o eixo
com o eixo 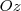 e é tangente a reta
e é tangente a reta  .
.
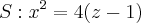 com o eixo
com o eixo 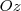 e é tangente a reta
e é tangente a reta  .
.




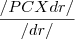 , sendo P um ponto de r, porém PC será um vetor nulo, uma vez que tem as mesmas coordenadas.
, sendo P um ponto de r, porém PC será um vetor nulo, uma vez que tem as mesmas coordenadas.