primeiro vc tem que ver quantos pontos tem no total
como cada lado tem dois pontos que estão sobre os vertices então vamos separar os vertices dos demais
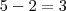


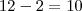
sendo que a soma toltal de pontos é dado pela soma dos pontos que estão sobre os lados e os quatro pontos sobre os vetices

agora tem que calcular o numero de combições de tres elementos que se forma com 29 elementos
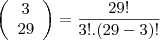
agora temos que para que tres pontos formem um triangula eles nao podem estar sobre um mesmo lado
então tem que se clacular o numero de combinação de 3 pontos em cada lado

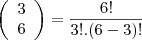

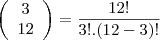
somando este quatro valores vc tera o total de combinações que não formam triangulos
subtraindo do total de combinações voce tera o numero que combinação que formam triangulos, dividindo pelo total voce tera probabilidade
B) para que ele seja diagonal pelo menos dois pontos tem que estar nos vertices opostos
que são duas combinações possiveis então



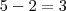



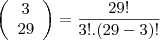

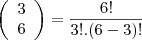

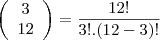


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.