 por heldersmd » Ter Set 18, 2012 20:03
por heldersmd » Ter Set 18, 2012 20:03
na questão:
Urn jogador langa dois dados honestos enquanto seu adversario lance apenas urn. Determine a probabilidade da soma dos pontos dos dois dados lancados pelo jogador ser igual aos pontos obtidos pelo dado langado pelo adversário.
No caso dos dados honestos temos uma probabilidade de 2/3 que podem ter o mesmo resultado do adversário.
Não sei se essa já é a resposta ou como posso introduzir esta probabilidade com o que se pede...
obrigado!!!!!!
-
heldersmd
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 14, 2012 16:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: vestibulando
- Andamento: cursando
 por young_jedi » Ter Set 18, 2012 22:26
por young_jedi » Ter Set 18, 2012 22:26
Pelo que eu entendi um jogador lança dois dados e o outro lança apenas, é isso?
se for voce tem que calcular quais são as combinações dos tres dados em que as soma dos dois primeiros é igual ao terceiro
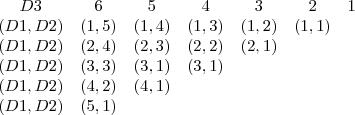
veja que voce tem 15 combinações sendo que o total de combinações entre os tres dados é 6.6.6 com isso vc acha a probabilidade
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por heldersmd » Ter Set 18, 2012 22:53
por heldersmd » Ter Set 18, 2012 22:53
heldersmd escreveu:na questão:
Urn jogador langa dois dados honestos enquanto seu adversario lance apenas urn. Determine a probabilidade da soma dos pontos dos dois dados lancados pelo jogador ser igual aos pontos obtidos pelo dado langado pelo adversário.
No caso dos dados honestos temos uma probabilidade de 2/3 que podem ter o mesmo resultado do adversário.
Não sei se essa já é a resposta ou como posso introduzir esta probabilidade com o que se pede...
obrigado!!!!!!
o que eu entendi é que são dois jogadores. o primeiro jogador tem dois dados normais e o outro tem 1 dado normal e outro viciado que sempre tira o numero 6.
-
heldersmd
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 14, 2012 16:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: vestibulando
- Andamento: cursando
 por MarceloFantini » Ter Set 18, 2012 23:13
por MarceloFantini » Ter Set 18, 2012 23:13
Isso não apareceu no enunciado. Você esqueceu de digitar algo?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por heldersmd » Ter Set 18, 2012 23:26
por heldersmd » Ter Set 18, 2012 23:26
heldersmd escreveu:heldersmd escreveu:na questão:
Urn jogador langa dois dados honestos enquanto seu adversario lance apenas urn. Determine a probabilidade da soma dos pontos dos dois dados lancados pelo jogador ser igual aos pontos obtidos pelo dado langado pelo adversário.
No caso dos dados honestos temos uma probabilidade de 2/3 que podem ter o mesmo resultado do adversário.
Não sei se essa já é a resposta ou como posso introduzir esta probabilidade com o que se pede...
obrigado!!!!!!
o que eu entendi é que são dois jogadores. o primeiro jogador tem dois dados normais e o outro tem 1 dado normal e outro viciado que sempre tira o numero 6.
É só isso mesmo...
talvez eu tenha entendido errado...
-
heldersmd
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 14, 2012 16:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: vestibulando
- Andamento: cursando
 por MarceloFantini » Ter Set 18, 2012 23:59
por MarceloFantini » Ter Set 18, 2012 23:59
Mas onde diz que o outro sempre tira 6? Isso é um ponto importante. Além disso, como não é especificado, poderia ser outro número, também alterando a soma. Se este é todo o enunciado, note que também não há menção sobre dados viciados. Apesar de ter dito que um lança dois dados honestos, ele teria de especificar se havia dados viciados em jogo, e "quão" viciados.
Por último, se houvesse tal dado ele deveria ter sido explícito dizendo "determine a probabilidade da soma dos pontos dos dois dados lançados pelo jogador ser igual aos pontos obtidos pela soma dos dados lançados pelo adversário", e não "determine a probabilidade da soma dos pontos dos dois dados lançados pelo jogador ser igual aos pontos obtidos pelo dado lançado pelo adversário."
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Lançamento de dado
por Ana Maria da Silva » Sáb Mar 22, 2014 20:04
- 2 Respostas
- 4251 Exibições
- Última mensagem por paulo testoni

Dom Jun 29, 2014 00:07
Probabilidade
-
- [Limite]no Ponto Dado
por eli83 » Sáb Out 06, 2012 14:16
- 1 Respostas
- 1223 Exibições
- Última mensagem por MarceloFantini

Sáb Out 06, 2012 14:33
Cálculo: Limites, Derivadas e Integrais
-
- Probabilidade (Lançamento de dado)
por tan lopes » Qui Out 25, 2012 17:06
- 2 Respostas
- 2660 Exibições
- Última mensagem por tan lopes

Ter Out 30, 2012 16:37
Probabilidade
-
- Lançamento simultâneo de dado
por zenildo » Seg Jul 13, 2015 00:22
- 0 Respostas
- 2663 Exibições
- Última mensagem por zenildo

Seg Jul 13, 2015 00:22
Probabilidade
-
- 18)Probabilidade e Estatística - Uma moeda e um dado...?
por Hellsius » Dom Abr 24, 2011 16:33
- 1 Respostas
- 1857 Exibições
- Última mensagem por NMiguel

Dom Abr 24, 2011 17:13
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


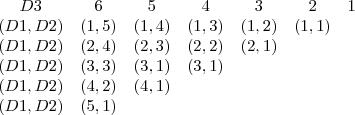




 .
.



