 por iceman » Dom Set 16, 2012 12:46
por iceman » Dom Set 16, 2012 12:46
Olá,
Poderia me ajudar com essa questão? Obrigado!

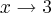
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Dom Set 16, 2012 12:49
por young_jedi » Dom Set 16, 2012 12:49
O problema de limite como esse é a divisão de zero por zero então vc tem que tentar contornar isso
então a dica para esse é encontrar as raizes do polinomio

e escreve-lo em função de suas raizes
e depois tentar simplificar a expressão
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por iceman » Dom Set 16, 2012 13:07
por iceman » Dom Set 16, 2012 13:07
young_jedi escreveu:O problema de limite como esse é a divisão de zero por zero então vc tem que tentar contornar isso
então a dica para esse é encontrar as raizes do polinomio

e escreve-lo em função de suas raizes
e depois tentar simplificar a expressão
Eu tenho problema na hora de fatorar pois eu não sei, ajuda?
meu professor tinha explicado mais ou menos assim:
Por exemplo eu tenho uma questão aqui respondida que ficou assim:



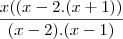
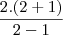
=
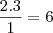
Aí depois faz Delta e Báscara, não vou fazer aqui se não vai ficar muito grande.
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Dom Set 16, 2012 13:10
por young_jedi » Dom Set 16, 2012 13:10
isso mesmo ele fatora as duas expressões e simplifica seus fatores comuns para depois aplicar o limite, no exercicio que vc postou deve utilizar o mesmo procedimento.
para fatorar vc encontra as raízes da equação.
sua forma fatorada vai ser o produto de x menos a raiz 1 pro x menos a raiz 2
observe

logo temos que a e b são raizes do polinomio
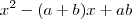
Editado pela última vez por
young_jedi em Dom Set 16, 2012 13:14, em um total de 1 vez.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por iceman » Dom Set 16, 2012 13:13
por iceman » Dom Set 16, 2012 13:13
young_jedi escreveu:isso mesmo ele fatora as duas expressões e simplifica seus fatores comuns para depois aplicar o limite, no exercicio que vc postou deve utilizar o mesmo procedimento.
Fica assim? :
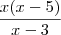
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por iceman » Dom Set 16, 2012 13:14
por iceman » Dom Set 16, 2012 13:14
iceman escreveu:young_jedi escreveu:isso mesmo ele fatora as duas expressões e simplifica seus fatores comuns para depois aplicar o limite, no exercicio que vc postou deve utilizar o mesmo procedimento.
Para fatorar fica assim? :
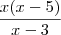
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Dom Set 16, 2012 13:21
por young_jedi » Dom Set 16, 2012 13:21
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por iceman » Dom Set 16, 2012 13:28
por iceman » Dom Set 16, 2012 13:28
Desculpa, E o primeiro processo de fatoração que eu tinha mostrado no exemplo ?
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Dom Set 16, 2012 13:35
por young_jedi » Dom Set 16, 2012 13:35
ele ele coloca x em evidencia primeiramente

e depois ele acha as raizees de
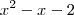
para escreve-lo de forma fatorada
e na segunda equação

ele ahca as raizes desta para escreve-la de forma fatorada
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por iceman » Dom Set 16, 2012 13:37
por iceman » Dom Set 16, 2012 13:37
young_jedi escreveu:ele ele coloca x em evidencia primeiramente

e depois ele acha as raizees de
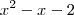
para escreve-lo de forma fatorada
e na segunda equação

ele ahca as raizes desta para escreve-la de forma fatorada
Mas não faz a mesma coisa nessa outra questão? Não se faz desse jeito ? Você fez tudo direto ?
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por iceman » Dom Set 16, 2012 13:39
por iceman » Dom Set 16, 2012 13:39
iceman escreveu:young_jedi escreveu:ele ele coloca x em evidencia primeiramente

e depois ele acha as raizees de
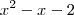
para escreve-lo de forma fatorada
e na segunda equação

ele ahca as raizes desta para escreve-la de forma fatorada
Mas não faz a mesma coisa nessa outra questão? Não se faz desse jeito ? Você fez tudo direto ?
Para fatorar não ficaria assim? :
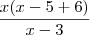
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Dom Set 16, 2012 13:39
por young_jedi » Dom Set 16, 2012 13:39
Voce pode fazer direto tambem se vc conseguir enxergar a forma fatorada só olhando para a função
caso não ai voce tem que calcular as raizes para encontrar sua forma fatorada
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por young_jedi » Dom Set 16, 2012 13:41
por young_jedi » Dom Set 16, 2012 13:41
Repare que em

não da para colocar x em evidencia visto que 6 nao esta multiplicado por x
então voce tem uma equação do segundo grau onde vc encontra sua forma fatorada achando as raizes
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por iceman » Dom Set 16, 2012 13:57
por iceman » Dom Set 16, 2012 13:57
young_jedi escreveu:Repare que em

não da para colocar x em evidencia visto que 6 nao esta multiplicado por x
então voce tem uma equação do segundo grau onde vc encontra sua forma fatorada achando as raizes
Para fazer a fatoração direto é preciso que todos os números estejam multiplicados por x? Se todos não estiverem multiplicados por x aí precisa fazer a equação do segundo grau, é isso? Seja para qualquer limite dessa forma?
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Dom Set 16, 2012 15:57
por young_jedi » Dom Set 16, 2012 15:57
SE todos os termos estiverem multiplicados por x isso quer dizer que x=0 é uma raiz do polinomio então voce ja tem uma raiz precisa achar as outras, e a resolução de equção do segundo grau é necessaria quando vc tem um termo com

, para voce fatorar voce tem que encontrar as raizes da equação, voce pode usar o metodo que voce quiser pra isso
o mais usual é por baskara porque todo mundo conhece e te da as duas raizes apenas aplicando a formula sem ter que fazer muitas analises
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5408 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4753 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4779 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4807 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2792 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

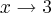


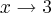

 e escreve-lo em função de suas raizes
e escreve-lo em função de suas raizes
e escreve-lo em função de suas raizes



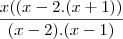
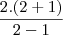 =
= 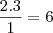


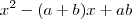

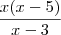


 então encontrando as raizes
então encontrando as raizes


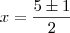
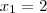


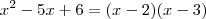

então encontrando as raizes


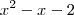 para escreve-lo de forma fatorada
para escreve-lo de forma fatorada ele ahca as raizes desta para escreve-la de forma fatorada
ele ahca as raizes desta para escreve-la de forma fatorada
para escreve-lo de forma fatorada
ele ahca as raizes desta para escreve-la de forma fatorada

para escreve-lo de forma fatorada
ele ahca as raizes desta para escreve-la de forma fatorada
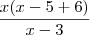





 , para voce fatorar voce tem que encontrar as raizes da equação, voce pode usar o metodo que voce quiser pra isso
, para voce fatorar voce tem que encontrar as raizes da equação, voce pode usar o metodo que voce quiser pra isso
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)