Acredito que tenha que fatorar a função, só que não obtive o resultado que é 2/3.
![\lim_{x \rightarrow 1}\frac{\sqrt[3]{x}-1}{\sqrt[2]{x}-1}](/latexrender/pictures/866ce432e04fb2278df602c6b997028e.png "\lim_{x \rightarrow 1}\frac{\sqrt[3]{x}-1}{\sqrt[2]{x}-1}")
Obrigado desde já
por will94 » Sáb Set 15, 2012 00:02
por MarceloFantini » Sáb Set 15, 2012 07:53
. Tiramos a raíz do numerador mas continuamos com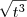 
no denominador. Se tentarmos 
também teremos o mesmo problema. Agora, o que poderíamos usar para cancelar ambos 2 e 3? O produto deles! Se 
, então teremos ![\lim_{x \to 1} \frac{\sqrt[3]{x} -1}{\sqrt{x} -1} = \lim_{t \to 1} \frac{t^2-1}{t^3-1}](/latexrender/pictures/be5dbd13f05ca4901cb8d60935632600.png "\lim_{x \to 1} \frac{\sqrt[3]{x} -1}{\sqrt{x} -1} = \lim_{t \to 1} \frac{t^2-1}{t^3-1}")
.
Voltar para Cálculo: Limites, Derivadas e Integrais
por roberto_trebor » Sáb Fev 15, 2014 20:45
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)