Bom, essa questão é do Programa de Avaliação Seriada da UnB, referente ao segundo ano. Eu estou com um pouco de dificuldade para resolvê-la e gostaria da ajuda de vocês.Sou nova aqui no fórum, por favor, se eu fizer algo de errado, tenham paciência comigo. Desde já, muito obrigada a todos que se prestarem a oferecer qualquer ajuda! ^^
Considere que, no esquema mostrado, a distância entre os
pontos A e B é igual a 4k, em que k é um número real positivo.
Considere, ainda, que esses pontos são simétricos em relação
à origem do sistema de coordenadas e que C = (0, -k). Com
base nesses dados, obtenha a equação da parábola que passa
pelos pontos A, B e C em função da constante k.
é uma constante Real e 
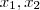são as raízes da mesma.
e 
são as intersecções da parábola com o eixo 
, isto é, suas abscissas são as raízes da equação da parábola. A saber, 
e 
, por exemplo.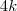
, isto é, 
, pois 
e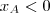 
portanto 
, e , como são simétricos, isto é, 
, temos o seguinte sistema:
e 
.
. 
pertence a essa parábola. Assim,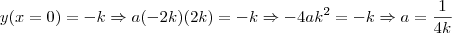
, uma vez que 
.
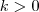. Ou então, 
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.