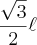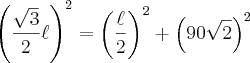por Dankaerte » Qui Ago 27, 2009 14:19
por Dankaerte » Qui Ago 27, 2009 14:19
A pirâmide de Quéops, em Gizé, no Egito, tem aproximadamente 90 raiz quadrada de 2 metros de altura, possui uma base quadrada e suas faces laterais são triângulos aquiláteros. Nessas condições, pode-se afirmar que, em metros, cada uma de suas arestas mede?
se alguém souber a fórmula e por ond começo para resolver esse exercício serei muito grato.
-
Dankaerte
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qua Ago 26, 2009 16:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qui Ago 27, 2009 14:58
por Molina » Qui Ago 27, 2009 14:58
Dankaerte escreveu:A pirâmide de Quéops, em Gizé, no Egito, tem aproximadamente 90 raiz quadrada de 2 metros de altura, possui uma base quadrada e suas faces laterais são triângulos aquiláteros. Nessas condições, pode-se afirmar que, em metros, cada uma de suas arestas mede?
se alguém souber a fórmula e por ond começo para resolver esse exercício serei muito grato.
Boa tarde, amigo.
Não sei se é o modo mais fácil, mas eu faria assim:
Já que temos que a pirâmide é formada por triângulos equiláteros podemos escrever a altura em função do lado:
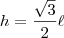
Essa fórmula é a altura do triângulo retângulo dos lados.
Não é a altura da pirâmide. Não podemos confundir a altura da pirâmide que é
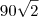
e a altura do triângulo das faces, que é
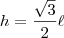
Fazendo um desenho, vemos que podemos chegar em um triângulo retângulo dentro da pirâmide, onde um dos catetos é a altura do triângulo das faces, o outro cateto é

e a hipotenusa é
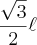
Usando Pitágoras:
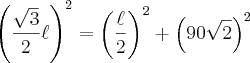
Resolvendo, chegamos em

Espero ter ajudado.
Caso tenha dúvida em alguma parte, avise!
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- preciso da Fórmula para resolver
por Dankaerte » Qui Ago 27, 2009 14:36
- 1 Respostas
- 5147 Exibições
- Última mensagem por Molina

Qui Ago 27, 2009 17:50
Estatística
-
- preciso de ajuda para resolver um exercicio sobre matrizes
por anabela » Sáb Nov 14, 2009 09:09
- 7 Respostas
- 7270 Exibições
- Última mensagem por Nelito

Seg Nov 16, 2009 16:56
Matrizes e Determinantes
-
- Preciso de uma explicação passo a passo para esse exercício
por Dankaerte » Qui Ago 27, 2009 14:24
- 0 Respostas
- 2256 Exibições
- Última mensagem por Dankaerte

Qui Ago 27, 2009 14:24
Sistemas de Equações
-
- É preciso saber limite para derivada e integral?
por mineirodointerior » Qui Out 15, 2015 00:34
- 2 Respostas
- 6860 Exibições
- Última mensagem por Cleyson007

Sáb Out 17, 2015 00:04
Cálculo: Limites, Derivadas e Integrais
-
- Preciso de ajuda com esse exercício
por Dankaerte » Qui Set 10, 2009 19:10
- 2 Respostas
- 6288 Exibições
- Última mensagem por Elcioschin

Ter Abr 13, 2010 14:01
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


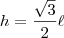
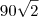 e a altura do triângulo das faces, que é
e a altura do triângulo das faces, que é  e a hipotenusa é
e a hipotenusa é