 por JKS » Sáb Ago 25, 2012 04:17
por JKS » Sáb Ago 25, 2012 04:17
Preciso de ajudaa..
(PUC) A inequação
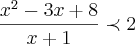
tem como solução o conjunto de números reais :
a)
![]-\infty,1[\cup]2,3[ ]-\infty,1[\cup]2,3[](/latexrender/pictures/7eedca16c61a765669a3274fa5095f0a.png)
b)
![]-\infty,-1]\cup[2,3] ]-\infty,-1]\cup[2,3]](/latexrender/pictures/93ddd108f0894ae8587270dedca460a5.png)
c)
![[2,3] [2,3]](/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png)
d)NENHUMA DAS RESPOSTAS ACIMA
____________________________________________________________________
Eu achei a) mas o gabarito está resposta >>>>>>> D) <<<<<<<<<< .. Não entendi
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Ago 25, 2012 10:38
por MarceloFantini » Sáb Ago 25, 2012 10:38
Para resolver esta inequação fazemos
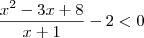
, daí
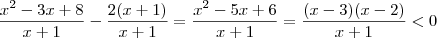
. Basta analisar o sinal.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Inequações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INEQUAÇÂO] Inequação do tipo: (a+ x < b + x < c + x)
por Diofanto » Dom Fev 03, 2013 19:55
- 7 Respostas
- 6296 Exibições
- Última mensagem por Diofanto

Qui Fev 14, 2013 23:45
Inequações
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7384 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- Inequação
por Luna » Seg Set 28, 2009 18:55
- 4 Respostas
- 3717 Exibições
- Última mensagem por Molina

Ter Set 29, 2009 16:50
Sistemas de Equações
-
- Inequação
por Luna » Ter Set 29, 2009 16:48
- 1 Respostas
- 2112 Exibições
- Última mensagem por Molina

Qua Set 30, 2009 00:39
Sistemas de Equações
-
- Inequação
por Bebel » Dom Ago 08, 2010 00:50
- 0 Respostas
- 1619 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
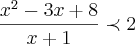 tem como solução o conjunto de números reais :
tem como solução o conjunto de números reais :![]-\infty,1[\cup]2,3[ ]-\infty,1[\cup]2,3[](/latexrender/pictures/7eedca16c61a765669a3274fa5095f0a.png)
![]-\infty,-1]\cup[2,3] ]-\infty,-1]\cup[2,3]](/latexrender/pictures/93ddd108f0894ae8587270dedca460a5.png)
![[2,3] [2,3]](/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png)


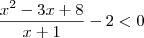 , daí
, daí 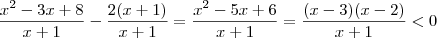 . Basta analisar o sinal.
. Basta analisar o sinal.
