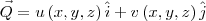 , onde
, onde  e
e  são funções lineares no espaço do tipo
são funções lineares no espaço do tipo  , que sou capaz de determinar.
, que sou capaz de determinar.E tenho três pontos no espaço,
 ,
,  e
e  . Notem que os pontos tem algumas coordenadas que se repetem, é assim mesmo.
. Notem que os pontos tem algumas coordenadas que se repetem, é assim mesmo.Meu problema é determinar o fluxo de
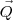 através da superfície triangular formada por ABC.
através da superfície triangular formada por ABC. Estou recorrendo à definição de integral do campo vetorial sobre uma superfície, que no meu caso pode ser escrita como
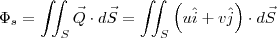
Para isso, eu determino a equação do plano que passa por A, B a C, do tipo
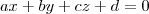 , onde as componentes do produto vetorial
, onde as componentes do produto vetorial  dão os valores dos coeficientes a, b e c, e o coeficiente d é obtido resolvendo-se a função para um dos pontos nesse plano, ou seja,
dão os valores dos coeficientes a, b e c, e o coeficiente d é obtido resolvendo-se a função para um dos pontos nesse plano, ou seja,  . Esse produto vetorial também me dá a orientação da superfície e, finalmente, o sentido do fluxo. Nesta página (em inglês) esse procedimento é descrito.
. Esse produto vetorial também me dá a orientação da superfície e, finalmente, o sentido do fluxo. Nesta página (em inglês) esse procedimento é descrito.Agora é que entra a minha dificuldade: não estou sabendo juntar tudo isso na integral.
Eu encontrei aqui (PDF em inglês; vide Example 2) um exemplo que descreve a solução de um exercício parecido com o meu. Lá, o sujeito parametriza a equação do plano, o que reduz o problema a uma integral múltipla com um produto escalar no integrando.
Eu não estou conseguindo fazer essa parametrização para o meu caso.
Alguém poderia, por favor, me ajudar a armar esta integral?
Como fazer devidamente a substituição de
 pela equação do plano?
pela equação do plano? Eu preciso realmente parametrizar esta equação? Tenho a impressão que não.
Obrigado!



 é uma porção triângular do plano
é uma porção triângular do plano  .
. e
e 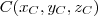 , não colineares, o plano que os contém tem um vetor normal
, não colineares, o plano que os contém tem um vetor normal  tal que
tal que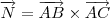 ,
,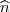 é então
é então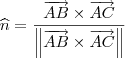 .
. e , de partida, o ponto A o plano é então
e , de partida, o ponto A o plano é então .
. .
. atráves da superfície
atráves da superfície 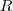 pertencente a
pertencente a  .
. , temos
, temos 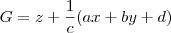 e, portanto,
e, portanto, . Ainda,
. Ainda,  .
.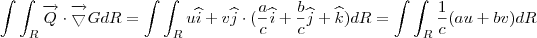
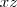 ou
ou  . Escolhamos o plano xz, por exemplo. A região será descrita , então, partindo da reta
. Escolhamos o plano xz, por exemplo. A região será descrita , então, partindo da reta  ,projeção em
,projeção em  , até a reta
, até a reta  , projeção
, projeção 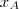 até a abcissa do ponto de intersecção das mesmas.
até a abcissa do ponto de intersecção das mesmas.

 de ambas.
de ambas.![\left\{\begin{matrix}
r_{BC}[y=0]:z=\frac{(z_C-z_B)}{(x_C-x_B)}x+z_B-x_B\frac{(z_C-z_B)}{(x_C-x_B)}\\
r_{AC}[y=0]:z=\frac{(z_C-z_A)}{(x_C-x_A)}x+z_A-x_A\frac{(z_C-z_A)}{(x_C-x_A)}
\end{matrix}\right.\Rightarrow \left\{\begin{matrix}
z_1=z_B+D_B(x-x_B)\\
z_2=z_A+D_A(x-x_A)
\end{matrix}\right. \left\{\begin{matrix}
r_{BC}[y=0]:z=\frac{(z_C-z_B)}{(x_C-x_B)}x+z_B-x_B\frac{(z_C-z_B)}{(x_C-x_B)}\\
r_{AC}[y=0]:z=\frac{(z_C-z_A)}{(x_C-x_A)}x+z_A-x_A\frac{(z_C-z_A)}{(x_C-x_A)}
\end{matrix}\right.\Rightarrow \left\{\begin{matrix}
z_1=z_B+D_B(x-x_B)\\
z_2=z_A+D_A(x-x_A)
\end{matrix}\right.](/latexrender/pictures/80f32d4b3da92f8a79eae7ec5ca33674.png)
![x_I=\frac{1}{(D_B-D_A)}\left [(z_B-z_A) +x_AD_A -x_BD_B\right ] x_I=\frac{1}{(D_B-D_A)}\left [(z_B-z_A) +x_AD_A -x_BD_B\right ]](/latexrender/pictures/501556ff11782791c49ce6f9fff6b07d.png)
![\pm \Phi =\int_{x_A}^{x_I}\int_{z_1(x)}^{z_2(x)}\frac{1}{c}(au[y=0]+bv[y=0])dzdx \pm \Phi =\int_{x_A}^{x_I}\int_{z_1(x)}^{z_2(x)}\frac{1}{c}(au[y=0]+bv[y=0])dzdx](/latexrender/pictures/2c4ed814c0f71401e2793df8c93101c8.png) .
.

 ,
,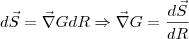 ?
?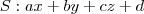 , não deveríamos ter
, não deveríamos ter  , e portanto
, e portanto  ? Com isso, teríamos
? Com isso, teríamos  . (A verdade é que nunca dominei essa notação com ":" que matemáticos usam para expressar funções)
. (A verdade é que nunca dominei essa notação com ":" que matemáticos usam para expressar funções) .
. é uma forma de resumir a formalmente correta
é uma forma de resumir a formalmente correta 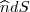 .
. de modo que
de modo que  ,
, 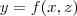 OU
OU 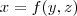 . Assim, a função
. Assim, a função  é uma SUPERFÍCIE DE NÍVEL construída da seguinte forma:
é uma SUPERFÍCIE DE NÍVEL construída da seguinte forma:  , para o 1° caso ,
, para o 1° caso ,  , para o segundo, OU
, para o segundo, OU  para o terceiro!
para o terceiro!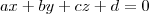 então ela é da forma
então ela é da forma  . Portanto,
. Portanto,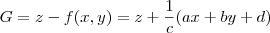 .
. em dois níveis verticais. Ou seja, um prisma triangular reto. Nos vértices desse prisma eu tenho os valores das componentes do campo vetorial. Veja que eu não tenho
em dois níveis verticais. Ou seja, um prisma triangular reto. Nos vértices desse prisma eu tenho os valores das componentes do campo vetorial. Veja que eu não tenho  e
e 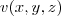 para todo
para todo 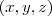 , mas apenas nas coordenadas dos vértices do prisma.
, mas apenas nas coordenadas dos vértices do prisma. 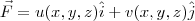 através da face superior do prisma, considerando que: (1) a integral da divergência desse campo sobre o volume do prisma é nula; (2) o fluxo através da face inferior (base) do prisma é nulo. Como eu não tenho fontes ou sumidouros de campo no interior do volume, o fluxo através da superfície fechada deve ser zero. Determinando o fluxo através de uma parte dessa superfície, fica determinado o fluxo no restante.
através da face superior do prisma, considerando que: (1) a integral da divergência desse campo sobre o volume do prisma é nula; (2) o fluxo através da face inferior (base) do prisma é nulo. Como eu não tenho fontes ou sumidouros de campo no interior do volume, o fluxo através da superfície fechada deve ser zero. Determinando o fluxo através de uma parte dessa superfície, fica determinado o fluxo no restante.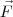 e calcular o fluxo através das faces laterais do prisma. Mas obter essa expressão demandaria demais do meu conhecimento em matemática, então eu optei por adotar funções lineares para ajustar as componentes do campo
e calcular o fluxo através das faces laterais do prisma. Mas obter essa expressão demandaria demais do meu conhecimento em matemática, então eu optei por adotar funções lineares para ajustar as componentes do campo  ,
, 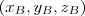 e
e  desse triangulo, valendo ressaltar que este triângulo não reside no plano mas sim no espaço. Não tenho certeza, mas tenho esperança que isso seja possível. Alguém poderia por favor fazer comentários a esse respeito?
desse triangulo, valendo ressaltar que este triângulo não reside no plano mas sim no espaço. Não tenho certeza, mas tenho esperança que isso seja possível. Alguém poderia por favor fazer comentários a esse respeito?
 ,
,  ,
,  e
e  :
: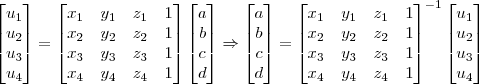
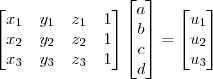
 (onde
(onde  se refere à cada um dos vértices do triângulo).
se refere à cada um dos vértices do triângulo).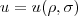 , o que me permitiria escrever um sistema de equações lineares solucionável. Algo do tipo
, o que me permitiria escrever um sistema de equações lineares solucionável. Algo do tipo
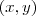 é referente a pontos pertencentes ao plano
é referente a pontos pertencentes ao plano  . Na verdade, os pontos deveriam ser expresso como
. Na verdade, os pontos deveriam ser expresso como  .
.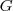 , terei um conteúdo diferente para o integrando.
, terei um conteúdo diferente para o integrando.
 , temos que
, temos que 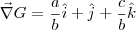
 , temos que
, temos que 
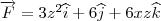 através da superfície
através da superfície  com
com  e
e  .
.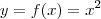 . Assim,
. Assim, 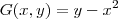 e
e  .
. e, assim,
e, assim, .
.