 por 20nho » Seg Ago 06, 2012 21:04
por 20nho » Seg Ago 06, 2012 21:04
Estava resolvendo uns exercícios de equação de 2º grau, mas na ultima pergunta veio uma conta que eu não soube resolver
A equação é a seguinte:
(x-1) (x² - 3x + 2) = (x-1) (2x - 4)
Alguém poderia me ajudar?
Agradeço.
-
20nho
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Ago 02, 2012 21:52
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Ago 06, 2012 21:20
por MarceloFantini » Seg Ago 06, 2012 21:20
Note que

, e
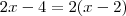
, daí
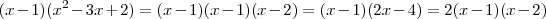
.
Isto mostra que a equação é válida para

,

e

. Vamos detalhar esta última passagem: se

, então

e tudo certo. Se

, podemos dividir por

ambos lados, gerando

. Se

, temos

e tudo certo. Se

, podemos dividir por

ambos lados, gerando

e finalmente

.
Obs.: Não existem graus de equações, o que existem são graus de polinômios. Neste caso, temos um polinômio de terceiro grau.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Talvez fatoração, mas não consegui desenvolver
por IsadoraLG » Qua Jul 09, 2014 21:13
- 1 Respostas
- 1189 Exibições
- Última mensagem por e8group

Qui Jul 10, 2014 00:58
Álgebra Elementar
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7716 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13209 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13014 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6091 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , e
, e 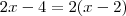 , daí
, daí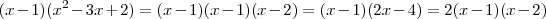 .
. ,
,  e
e  . Vamos detalhar esta última passagem: se
. Vamos detalhar esta última passagem: se  , então
, então  e tudo certo. Se
e tudo certo. Se  , podemos dividir por
, podemos dividir por  ambos lados, gerando
ambos lados, gerando  . Se
. Se  , temos
, temos  e tudo certo. Se
e tudo certo. Se  , podemos dividir por
, podemos dividir por  ambos lados, gerando
ambos lados, gerando  e finalmente
e finalmente  .
.

