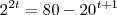por llslucas3 » Ter Jul 31, 2012 12:47
por llslucas3 » Ter Jul 31, 2012 12:47
Se as trajetórias de dois móveis são dadas por Sa =
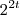
e Sb =
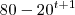
, determine em quanto tempo eles de encontram, ou seja, quando Sa = Sb.
-
llslucas3
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jul 31, 2012 10:47
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso técnico em química
- Andamento: cursando
 por Russman » Ter Jul 31, 2012 17:20
por Russman » Ter Jul 31, 2012 17:20
As funções formam o sistema
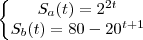
.
Precisamos calcular para qual

que

. Assim,
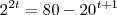
Eu desconheço um método analítico para esta solução. Assim, veja este link :
http://www.wolframalpha.com/input/?i=2^%282t%29+%3D+80+-+20^%28t%2B1%29
P.S.: ao invés de 20, na equação não seria 2?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1625 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2840 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2829 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2242 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2193 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
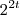 e Sb =
e Sb = 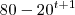 , determine em quanto tempo eles de encontram, ou seja, quando Sa = Sb.
, determine em quanto tempo eles de encontram, ou seja, quando Sa = Sb.
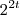 e Sb =
e Sb = 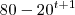 , determine em quanto tempo eles de encontram, ou seja, quando Sa = Sb.
, determine em quanto tempo eles de encontram, ou seja, quando Sa = Sb.
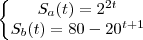 .
. que
que  . Assim,
. Assim,