 por Claudin » Seg Jul 09, 2012 19:50
por Claudin » Seg Jul 09, 2012 19:50
Determine a equação do plano definido pelo ponto

e pela reta
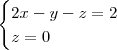
Não sei como iniciar o exercício, gostaria de uma dica para iniciar.
Tenho que tirar vetor diretor da reta e aplicar nos pontos para achar equação do plano?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Seg Jul 16, 2012 03:55
por Claudin » Seg Jul 16, 2012 03:55
Ainda não sei como resolver
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Ter Jul 17, 2012 03:00
por Claudin » Ter Jul 17, 2012 03:00
Ainda não sei como resolver[2]
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Ter Jul 17, 2012 04:31
por Russman » Ter Jul 17, 2012 04:31
Eu começaria parametrizando a reta!
Depois disso, basta proceder como você faz quando tem uma reta parametrizada e um ponto.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Claudin » Ter Jul 17, 2012 18:59
por Claudin » Ter Jul 17, 2012 18:59
Como assim parametrizando? Poderia me dar o exemplo Rusman, pois eu tenho um ponto e tenho o vetor diretor da reta, para parametrizar não seria necessário ter dois pontos?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Ter Jul 17, 2012 19:01
por Russman » Ter Jul 17, 2012 19:01
Uma parametrização possível é, de uma forma bem simples, tomar

. Assim, isole o

em função de

, isto é,

. A equação paramétrica do

você já tem, que é
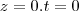
.

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Claudin » Sex Jul 20, 2012 03:29
por Claudin » Sex Jul 20, 2012 03:29
Encontrei duas equações
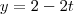
e

E depois?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Seg Jul 23, 2012 21:05
por Claudin » Seg Jul 23, 2012 21:05
?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Seg Jul 23, 2012 23:34
por Russman » Seg Jul 23, 2012 23:34
Agora você tem um ponto e a reta
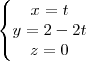
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MarceloFantini » Ter Jul 24, 2012 03:49
por MarceloFantini » Ter Jul 24, 2012 03:49
Acho que você errou algumas contas:
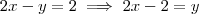
;
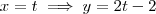
e não
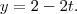
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Qua Jul 25, 2012 16:13
por Claudin » Qua Jul 25, 2012 16:13
Isso mesmo Marcelo Fantini.

Tendo um ponto e uma reta paramétrica, como chegar na equação do plano
cartesiana?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Qua Jul 25, 2012 17:09
por Claudin » Qua Jul 25, 2012 17:09
?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por hygorvv » Qui Jul 26, 2012 14:50
por hygorvv » Qui Jul 26, 2012 14:50
Eu faria diferente. Minha contribuição:
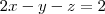

Logo,
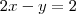
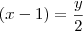

(Equações simétricas da reta)
Equação vetorial da reta :
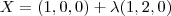
Agora você tem dois pontos e um vetor paralelo ao plano.
Veja se te ajuda.
-
hygorvv
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Ter Jun 05, 2012 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Qui Jul 26, 2012 20:16
por DanielFerreira » Qui Jul 26, 2012 20:16
E aí Hygorvv, blz?
seja bem-vindo!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por hygorvv » Sex Jul 27, 2012 00:27
por hygorvv » Sex Jul 27, 2012 00:27
Valeu, danjr5!

-
hygorvv
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Ter Jun 05, 2012 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Claudin » Sex Jul 27, 2012 00:44
por Claudin » Sex Jul 27, 2012 00:44
hygorvv escreveu:Eu faria diferente. Minha contribuição:
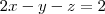

Logo,
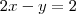
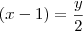

(Equações simétricas da reta)
Equação vetorial da reta :
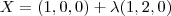
Agora você tem dois pontos e um vetor paralelo ao plano.
Veja se te ajuda.
O problema é que pede equação na forma cartesiana e não vetorial.
Mas obrigado pela ajuda, e obrigado a todos
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por hygorvv » Sex Jul 27, 2012 00:57
por hygorvv » Sex Jul 27, 2012 00:57
Sim, com dois pontos e um vetor paralelo você consegue a equação geral do plano.
-
hygorvv
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Ter Jun 05, 2012 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Claudin » Sex Jul 27, 2012 01:03
por Claudin » Sex Jul 27, 2012 01:03
Sim.
Mas como você encontrou o ponto

?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por hygorvv » Sex Jul 27, 2012 01:19
por hygorvv » Sex Jul 27, 2012 01:19
Olha as equações simétricas da reta. Sendo uma equação vetorial de uma reta sendo
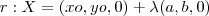
, suas equações simétricas(ou reduzidas) serão:
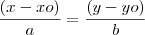
e

Tenta comparar agora.
Espero que te ajude.
-
hygorvv
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Ter Jun 05, 2012 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Sáb Jul 28, 2012 13:56
por LuizAquino » Sáb Jul 28, 2012 13:56
Claudin escreveu:Mas como você encontrou o ponto

?
Sala de Bate Papo - 28 de julho de 2012(10:55:48)
Claudin: Luiz Aquino, poderia me ajudar no tópico plano, nao consegui enxergar o ponto 1,0,0
O procedimento é simples. Basta analisar as equações.
Sabemos que a reta é a interseção dos planos 2x - y - z = 2 e z = 0. Isso significa que todos os pontos dessa reta devem atender essas duas equações.
Analisando a segunda delas, note que sempre a coordenada z é igual a zero. Sendo assim, já sabemos que todos os pontos dessa reta possuem o formato P = (x, y, 0).
Substituindo então z = 0 na primeira equação, obtemos que y = 2x - 2. Ou seja, podemos dizer que todos os pontos da reta possuem o formato P = (x, 2x - 2, 0). Note que escolhendo um valor qualquer para x podemos encontrar o valor correspondente para a coordenada y.
Agora responda: que ponto é obtido quando escolhemos x = 1?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sáb Jul 28, 2012 14:12
por Claudin » Sáb Jul 28, 2012 14:12
Sim, iria encontrar (1,0,0)
Obrigado a todos pelas explicações.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Sex Ago 31, 2012 21:14
por Claudin » Sex Ago 31, 2012 21:14
Tendo como vetor (1,2,0) e como ponto P(2,1,3)
Para encontrar a equação do plano na forma cartesiana, acabei substituindo na equação
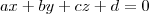
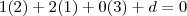

Porém a equação correta no gabarito não é essa.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sex Ago 31, 2012 21:38
por LuizAquino » Sex Ago 31, 2012 21:38
Claudin escreveu:Tendo como vetor (1,2,0) e como ponto P(2,1,3)
Para encontrar a equação do plano na forma cartesiana, acabei substituindo na equação
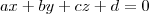
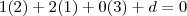

Porém a equação correta no gabarito não é essa.
Na equação do plano, os coeficientes a, b e c representam as coordenadas de um vetor normal ao plano. Acontece que
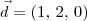
não é um vetor normal ao plano!
Analise a figura abaixo. Você já conhece P = (2,1,3) e
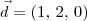
. Para determinar um vetor

normal ao plano, basta calcular
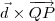
, sendo Q um ponto qualquer da reta r. Tente continuar a partir daí.

- figura.png (3.09 KiB) Exibido 13337 vezes
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sáb Set 01, 2012 03:41
por Claudin » Sáb Set 01, 2012 03:41
Obrigado pela explicação

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações de plano] encontrar a equação de um plano
por GHT1810 » Ter Jul 03, 2018 19:42
- 0 Respostas
- 5367 Exibições
- Última mensagem por GHT1810

Ter Jul 03, 2018 19:42
Geometria Analítica
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14966 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
-
- [Equação do Plano Tangente - Plano Paralalelo]
por raimundoocjr » Qui Out 24, 2013 22:10
- 0 Respostas
- 2945 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- Plano
por Rhyu » Dom Abr 08, 2012 10:57
- 2 Respostas
- 1999 Exibições
- Última mensagem por MarceloFantini

Seg Abr 09, 2012 03:40
Geometria Analítica
-
- Plano
por Claudin » Sex Jul 06, 2012 12:32
- 2 Respostas
- 1817 Exibições
- Última mensagem por Claudin

Sex Jul 06, 2012 16:23
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e pela reta
e pela reta 

 e pela reta
e pela reta 



 . Assim, isole o
. Assim, isole o  em função de
em função de  , isto é,
, isto é,  . A equação paramétrica do
. A equação paramétrica do  você já tem, que é
você já tem, que é 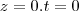 .
.







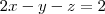

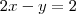
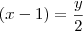
 (Equações simétricas da reta)
(Equações simétricas da reta)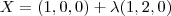


(Equações simétricas da reta)

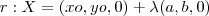 , suas equações simétricas(ou reduzidas) serão:
, suas equações simétricas(ou reduzidas) serão: 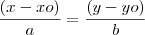 e
e 

?



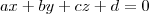
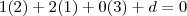


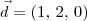 não é um vetor normal ao plano!
não é um vetor normal ao plano!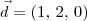 . Para determinar um vetor
. Para determinar um vetor  normal ao plano, basta calcular
normal ao plano, basta calcular 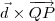 , sendo Q um ponto qualquer da reta r. Tente continuar a partir daí.
, sendo Q um ponto qualquer da reta r. Tente continuar a partir daí.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
