Maligno, mas podemos chegar àquelas conclusões começando quase assim mesmo.
Minha sugestão é numerar os 50 estudantes (em colunas).
Para cada estudante, anote os armários que ele inverteu (em linhas).
1ª conclusão) Como o aluno 1 abriu todos os armários, a cada vez que um número de armário reaparece (mudando as colunas), a posição da porta do armário é invertida. Logo, se um certo armário aparecer um número
par de vezes do aluno 1 ao 50, então este armário ficou
fechado. Se aparecer um número
ímpar de vezes, ele ficou
aberto.
2ª conclusão) Já assim facilita, mas ainda podemos perceber outra peculiaridade para não ficarmos contando.
Repare no número de cada armário e na quantidade de vezes que ele aparece. Tentando relacionar este números, percebemos que a quantidade de vezes que ele aparece é também a quantidade de divisores inteiros que ele possui.
Exemplos:
O armário 2 aparece duas vezes e possui dois divisores
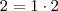
.
O armário 4 aparece 3 vezes,
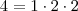
, os divisores são 1, 2 e 4, logo, fica aberto.
Vamos considerar um armário mais adiante...
O armário 32, quantas vezes aparece? Sem mais contar, pensemos nos divisores,

. Os divisores são 1, 2, 4, 8, 16 e 32. Um número par de divisores, então ele fica fechado, aparece 6 vezes.
Note que todos os armários cujos números são primos aparecem apenas duas vezes, portanto, também ficam fechados.
Este procedimento é mais prático pois a quantidade divisores não é grande para cada número de armário.
Por exemplo, entre 1 e 50, 48 é o que tem mais divisores, possui 10. Os demais ficam abaixo disso, sendo a maioria com 2, 3 ou 4.
Até mais!







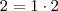 .
.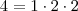 , os divisores são 1, 2 e 4, logo, fica aberto.
, os divisores são 1, 2 e 4, logo, fica aberto. . Os divisores são 1, 2, 4, 8, 16 e 32. Um número par de divisores, então ele fica fechado, aparece 6 vezes.
. Os divisores são 1, 2, 4, 8, 16 e 32. Um número par de divisores, então ele fica fechado, aparece 6 vezes.




 , avisa que eu resolvo.
, avisa que eu resolvo.

