Eu preciso que o ângulo da câmera mude em função da velocidade de um personagem.
As condições são as seguintes:
Quando a velocidade for menor ou igual a 150 Unidades de Velocidade, o valor do ângulo seja 342.
Quando a velocidade seja 522, o ângulo tem de ser 332.
No um intervalo entre 150 e 522, o angulo tem que corresponder a um valor da velocidade, ou seja, a troca de ângulos tem que ser 'suavemente', e não repentinamente como se trocasse o angulo somente ao chegar aos 522.
Acho que a solução seria fazer uma equação do ângulo em função da velocidade. O detalhe é que obviamente não seria algo linear. Se fosse eu saberia como criar uma equação, mas como não é, eu não sei como montá-la. Como procedo?
Muito Obrigado!
*Atualização
Acho que dá pra fazer algo linear, sim.
1)Faço uma função onde quando
 o angulo dá 342
o angulo dá 3422)Quando v for entre
![]150,522] ]150,522]](/latexrender/pictures/b15b603a57107f3af0e77c4083d2fe9b.png) o angulo cresce em uma função linear, onde quando v é 150, o angulo é 342; quando o v é 522, o angulo é 332.
o angulo cresce em uma função linear, onde quando v é 150, o angulo é 342; quando o v é 522, o angulo é 332.Porém, por mais que eu tenha tentado, não consegui achar uma equação que satisfaça a segunda.
Agradeço



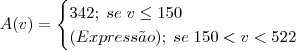
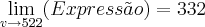 , e
, e 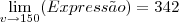 .
.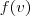 que contenha em seu gráfico os pontos
que contenha em seu gráfico os pontos 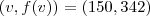 e
e 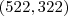 .
.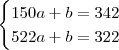

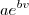 . Novamente o que você precisa fazer é determinar os coeficientes a e b, lembrando que a função deve passar pelos pontos (150, 342) e (522, 322). Para isso, basta resolver o sistema:
. Novamente o que você precisa fazer é determinar os coeficientes a e b, lembrando que a função deve passar pelos pontos (150, 342) e (522, 322). Para isso, basta resolver o sistema:
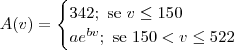

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.