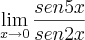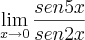por Allysom » Sáb Jun 23, 2012 17:39
por Allysom » Sáb Jun 23, 2012 17:39
Bom galera, eu estou com dificuldades na resolução desses limites. E peguei todas as explicações de meu professor, mais mesmo assim continua vago para mim .
a)
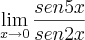
-
Allysom
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mar 14, 2012 04:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: si
- Andamento: cursando
 por Russman » Sáb Jun 23, 2012 19:23
por Russman » Sáb Jun 23, 2012 19:23
Você conhece o Teorema de l'Hôpital? Se não, segue o link abaixo.
http://pt.wikipedia.org/wiki/Regra_de_l'H%C3%B4pitalEntão, veja que se x=0 voê obtem uma indeterminação do tipo 0/0. Assim, derivando ambos os membros, obtemos
lim (sin(ax))/(sin(bx)) = lim (a.cos(ax))/(b.cos(bx)) .
Agora, quando x=0 temos a/b pois cos(a.0) = cos(0) = 1 e cos(b.0)=cos(0) = 1.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Allysom » Sáb Jun 23, 2012 19:41
por Allysom » Sáb Jun 23, 2012 19:41
Muito obrigado por responder. Bem eu ainda não aprendi a derivar , mas o meu professor me deu este limite como base para respondelo.

-
Allysom
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mar 14, 2012 04:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: si
- Andamento: cursando
 por Russman » Sáb Jun 23, 2012 19:54
por Russman » Sáb Jun 23, 2012 19:54
Se você quiser usar este limite então proceda assim:

Entende? Se tiver dúvida em algum passo, pergunte.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas e curiosidade com os limites fundamentais
por Luthius » Seg Ago 03, 2009 11:29
- 4 Respostas
- 4216 Exibições
- Última mensagem por Luthius

Ter Ago 04, 2009 08:44
Cálculo: Limites, Derivadas e Integrais
-
- aplicação das relações fundamentais
por Apotema » Qui Nov 26, 2009 12:23
- 2 Respostas
- 1696 Exibições
- Última mensagem por Apotema

Qui Nov 26, 2009 16:01
Trigonometria
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4750 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4774 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.