Tenho este exercicio:
Uma fábrica incorpora na sua produção um certo tipo de peças, que compra a três fornecedores( fornecedor I, fornecedor II, fornecedor III) nas seguintes proporções: 0.4 , 0.35 e 0.25. Da experiência passada, os responsáveis da fábrica sabem que 2% das peças oriundas do fornecedor I são defeituosas euq e essa percentagem é de 5% para o fornecedor II; sabem, ainda que 3.55% da totalidade de peças, deste tipo, que compram são defeituosas.
Calcule a percentagem de peças defeituosas fornecidas pelo fornecedor III.
Eu estava a fazer que
x----------3.55%
25%---------100%
(3.55 * 25)/100 = 0.88
Também já fiz que :
2----------100
x----------3.55
(2*3.55)/100= 0.071
5----------100
x----------3.55
(5*3.55)/100=0.1775
Depois fiz : 0.071+0.1775+ x = 3.55 <=> x= 3.30 a percentagem de defeito da III, gostaria que me dissessem se está bem ou mal, e que me ajudem sff!
Acho que está mal, não estou a conseguir achar essa percentagem de nenhuma maneira.


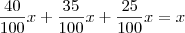 .
. . Ou Seja , z = 4 % .
. Ou Seja , z = 4 % .
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)