 por Jhonata » Qua Jun 20, 2012 10:44
por Jhonata » Qua Jun 20, 2012 10:44
Não consigo nada na seguinte questão:
Seja

a região limitada entre

e o eixo-x. Encontre a equação da reta que passa pela origem e que divide

em duas subregiões com áreas iguais.
Eu tentei resolver de muitas formas, mas não consigo progredir nada nessa questão; tudo que consegui fazer foi esboçar o gráfico da função, encontrar o ponto crítico, os pontos de interseção e sua área entre esses pontos
.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por Russman » Qua Jun 20, 2012 11:13
por Russman » Qua Jun 20, 2012 11:13
Seja a a reta uma função
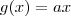
.
A área superior da parábola, que chamarei de
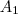
é dada por
![A_{1} = \int_{0}^{k}[ f(x) - g(x)] A_{1} = \int_{0}^{k}[ f(x) - g(x)]](/latexrender/pictures/f17b1f1c0195dc126d2ec2d4488bd2de.png)
,
pois

no intervalo
![[0,k] [0,k]](/latexrender/pictures/6c279203fd44ea566ecb1778414e009b.png)
.
O valor

é onde as funções se intersectam. Assim,
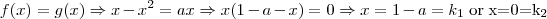
O valor nulo para

ja era conhecido, pois a reta passa pela origem.
A area que sobra, a area 2,

é dada pela soma da area do triângulo e de um pedaço da parábola. Ou então, pela area que sobra.
![A_{2} = \int_{0}^{1} f(x) - A_{1} = \int_{0}^{1} f(x) - \int_{0}^{k} [f(x) - g(x)] A_{2} = \int_{0}^{1} f(x) - A_{1} = \int_{0}^{1} f(x) - \int_{0}^{k} [f(x) - g(x)]](/latexrender/pictures/97f1390260e0b7e58e4f72e556c01893.png)
.
Agora é só fazer

efetuar a integrais e isolar

que você descobre a reta.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qua Jun 20, 2012 14:07
por Russman » Qua Jun 20, 2012 14:07
Eu fiz as contas aqui e cheguei em
![a = 1 + \frac{1}{\sqrt[3]{2}} a = 1 + \frac{1}{\sqrt[3]{2}}](/latexrender/pictures/d17e3ad76a8bfdb91372291fe9bc66cd.png)
.
Portanto a reta é
![g(x) = (1 + \frac{1}{\sqrt[3]{2}})x g(x) = (1 + \frac{1}{\sqrt[3]{2}})x](/latexrender/pictures/806cf91474aa89565ea9f1d6ded0f2e0.png)
.
Veja se você chega no mesmo resultado.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área entre curvas. Sen(x) e x³ em [0, pi]. Alguém ajuda?
por vmoura » Dom Abr 02, 2017 17:56
- 0 Respostas
- 3042 Exibições
- Última mensagem por vmoura

Dom Abr 02, 2017 17:56
Cálculo: Limites, Derivadas e Integrais
-
- Área comum as curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:00
- 0 Respostas
- 1052 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 23, 2014 22:00
Cálculo: Limites, Derivadas e Integrais
-
- Integrais e área entre curvas
 por Victor Mello » Ter Nov 19, 2013 21:58
por Victor Mello » Ter Nov 19, 2013 21:58
- 2 Respostas
- 2007 Exibições
- Última mensagem por Victor Mello

Qua Nov 20, 2013 00:28
Cálculo: Limites, Derivadas e Integrais
-
- Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:02
- 0 Respostas
- 1128 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 23, 2014 22:02
Cálculo: Limites, Derivadas e Integrais
-
- Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:04
- 1 Respostas
- 1509 Exibições
- Última mensagem por matmatco

Sáb Ago 09, 2014 12:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 a região limitada entre
a região limitada entre  e o eixo-x. Encontre a equação da reta que passa pela origem e que divide
e o eixo-x. Encontre a equação da reta que passa pela origem e que divide  em duas subregiões com áreas iguais.
em duas subregiões com áreas iguais.

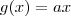 .
.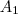 é dada por
é dada por![A_{1} = \int_{0}^{k}[ f(x) - g(x)] A_{1} = \int_{0}^{k}[ f(x) - g(x)]](/latexrender/pictures/f17b1f1c0195dc126d2ec2d4488bd2de.png) ,
, no intervalo
no intervalo ![[0,k] [0,k]](/latexrender/pictures/6c279203fd44ea566ecb1778414e009b.png) .
. é onde as funções se intersectam. Assim,
é onde as funções se intersectam. Assim,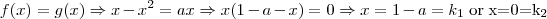
 ja era conhecido, pois a reta passa pela origem.
ja era conhecido, pois a reta passa pela origem. é dada pela soma da area do triângulo e de um pedaço da parábola. Ou então, pela area que sobra.
é dada pela soma da area do triângulo e de um pedaço da parábola. Ou então, pela area que sobra.![A_{2} = \int_{0}^{1} f(x) - A_{1} = \int_{0}^{1} f(x) - \int_{0}^{k} [f(x) - g(x)] A_{2} = \int_{0}^{1} f(x) - A_{1} = \int_{0}^{1} f(x) - \int_{0}^{k} [f(x) - g(x)]](/latexrender/pictures/97f1390260e0b7e58e4f72e556c01893.png) .
. efetuar a integrais e isolar
efetuar a integrais e isolar  que você descobre a reta.
que você descobre a reta.
![a = 1 + \frac{1}{\sqrt[3]{2}} a = 1 + \frac{1}{\sqrt[3]{2}}](/latexrender/pictures/d17e3ad76a8bfdb91372291fe9bc66cd.png) .
.![g(x) = (1 + \frac{1}{\sqrt[3]{2}})x g(x) = (1 + \frac{1}{\sqrt[3]{2}})x](/latexrender/pictures/806cf91474aa89565ea9f1d6ded0f2e0.png) .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.