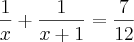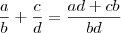por LuizCarlos » Sex Jun 15, 2012 16:14
por LuizCarlos » Sex Jun 15, 2012 16:14
Olá amigos do fórum, gostaria de uma ajuda nesses dois exercícios!

Estou tendo dificuldades para encontrar o m.m.c!
Tentei encontrar, achei:

. Está certo esse m.m.c.
Tem esse exercício aqui também!
Determine dois números inteiros, positivos e consecutivos, cuja soma dos inversos seja
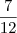
.
Tentei resolver dessa maneira:
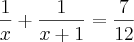
Encontrei m.m.c =

-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Russman » Sex Jun 15, 2012 19:34
por Russman » Sex Jun 15, 2012 19:34
Bom, vou te dar uma dica q eu sempre sugiro aos meus alunos!
Na álbegra, é fato que
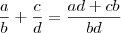
Ou seja, o M.M.C. dos denominadores serve para que se extraia a fração reduzida da operação. Mas se você não calcular o M.M.C. e simplismente "multiplicar em cruz" os denominadores vai estar "fazendo certo" da mesma forma.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por DanielFerreira » Sex Jun 15, 2012 20:46
por DanielFerreira » Sex Jun 15, 2012 20:46
LuizCarlos escreveu:Olá amigos do fórum, gostaria de uma ajuda nesses dois exercícios!

Estou tendo dificuldades para encontrar o m.m.c!
Tentei encontrar, achei:

. Está certo esse m.m.c.
(4 - x) ___________ 8 ___________ x | (4 - x)
1 _______________ 8 ___________ x | 8
1 _______________ 1 ___________ x | x
1 _______________ 1 ___________ 1 |
MMC(4 - x, 8, x) =
8x(4 - x)"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Sex Jun 15, 2012 20:52
por DanielFerreira » Sex Jun 15, 2012 20:52
LuizCarlos escreveu:Olá amigos do fórum, gostaria de uma ajuda nesses dois exercícios!
Tem esse exercício aqui também!
Determine dois números inteiros, positivos e consecutivos, cuja soma dos inversos seja
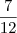
.
Tentei resolver dessa maneira:
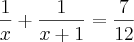
Encontrei m.m.c =

(x + 1)___________ 12 ___________ x | (x + 1)
1 _______________ 12 ___________ x | 12
1 _______________ 1 ____________ x | x
1 _______________ 1 ___________ 1 |
MMC(x + 1, 12, x) =
12x(x + 1) Luiz Carlos,
lembre-se que o MMC entre os números primos entre si é igual ao produto entre eles, veja:
MMC(2,3,5) = 2 . 3 . 5
MMC(2,3,5) = 30
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizCarlos » Sáb Jun 16, 2012 13:30
por LuizCarlos » Sáb Jun 16, 2012 13:30
Russman escreveu:Bom, vou te dar uma dica q eu sempre sugiro aos meus alunos!
Na álbegra, é fato que
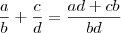
Ou seja, o M.M.C. dos denominadores serve para que se extraia a fração reduzida da operação. Mas se você não calcular o M.M.C. e simplismente "multiplicar em cruz" os denominadores vai estar "fazendo certo" da mesma forma.
Obrigado, consegui entender Russman!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Sáb Jun 16, 2012 13:31
por LuizCarlos » Sáb Jun 16, 2012 13:31
danjr5 escreveu:LuizCarlos escreveu:Olá amigos do fórum, gostaria de uma ajuda nesses dois exercícios!

Estou tendo dificuldades para encontrar o m.m.c!
Tentei encontrar, achei:

. Está certo esse m.m.c.
(4 - x) ___________ 8 ___________ x | (4 - x)
1 _______________ 8 ___________ x | 8
1 _______________ 1 ___________ x | x
1 _______________ 1 ___________ 1 |
MMC(4 - x, 8, x) =
8x(4 - x)
Valeu amigo danjr5, consegui entender, não sei como consigo ficar em dúvida em m.m.c já fiz tantos exercícios desses!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação do segundo grau
por VtinxD » Qui Jan 27, 2011 23:03
- 1 Respostas
- 3887 Exibições
- Última mensagem por douglaspezzin

Dom Jun 19, 2011 09:55
Desafios Médios
-
- Equação de segundo grau
por maria cleide » Seg Mai 09, 2011 23:46
- 3 Respostas
- 2685 Exibições
- Última mensagem por FilipeCaceres

Ter Mai 10, 2011 00:43
Sistemas de Equações
-
- Equação do segundo grau
por LuizCarlos » Qui Mai 10, 2012 13:01
- 3 Respostas
- 3102 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 12, 2012 20:41
Álgebra Elementar
-
- equaçao de segundo grau
por will140592 » Dom Mar 03, 2013 11:40
- 1 Respostas
- 2538 Exibições
- Última mensagem por Russman

Dom Mar 03, 2013 19:45
Álgebra Linear
-
- equaçao de segundo grau
por will140592 » Dom Mar 03, 2013 20:21
- 1 Respostas
- 1815 Exibições
- Última mensagem por Russman

Dom Mar 03, 2013 20:43
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 . Está certo esse m.m.c.
. Está certo esse m.m.c.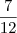 .
.