 por Claudin » Ter Jun 12, 2012 20:46
por Claudin » Ter Jun 12, 2012 20:46
Dada a parábola
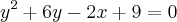
, determine os valores de

para que a reta

a) Seja secante à parábola
b) Seja tangente à parábola
c) Não corte a parábola
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Jun 13, 2012 10:39
por LuizAquino » Qua Jun 13, 2012 10:39
Claudin escreveu:Dada a parábola
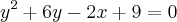
, determine os valores de

para que a reta

a) Seja secante à parábola
b) Seja tangente à parábola
c) Não corte a parábola
Basta utilizar o mesmo raciocínio que lhe foi explicado em seu outro tópico:
Elipseviewtopic.php?f=117&t=8483
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qua Jun 13, 2012 21:09
por Claudin » Qua Jun 13, 2012 21:09
Não consegui resolver o exercício.
Encontrei essa equação quando substitui o valor do

na equação.
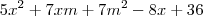
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Jun 14, 2012 14:46
por LuizAquino » Qui Jun 14, 2012 14:46
Claudin escreveu:Não consegui resolver o exercício.
Encontrei essa equação quando substitui o valor do

na equação.
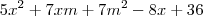
Fazendo a substituição
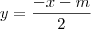
, você deveria obter:
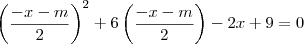
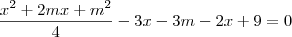
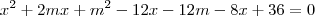
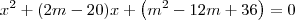
Considerando isso como uma equação polinomial do 2° grau na incógnita
x, calcule o discriminante

. Em seguida, use a análise que lhe foi explicada em seu outro tópico.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Jun 14, 2012 15:07
por Claudin » Qui Jun 14, 2012 15:07
Mas no caso, o meu "c" da equação do segundo grau quando for calcular o delta, seria uma nova equação do segundo grau, ou seja, irei obter dois valores para c?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Qui Jun 14, 2012 20:02
por Russman » Qui Jun 14, 2012 20:02
Nãao. Os valores "c" da equação de 2° grau em x que foi calculada dependem dos valores "m" de acordo com a relação
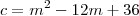
.
Ainda,

e
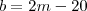
.
Com isso, o discriminate

da equação é
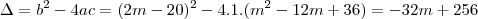
.
É crucial o calculo do discriminante pois é ele que comanda o tipo de solução que a equação terá. Veja que para a reta ser secante ao gráfico devem exixtir dois pontos de intersecção, ou seja, dois valores para x. Fazendo

isto é garantido. Já, para a reta ser tangente deve existir apenas um ponto de intersecção que é garantido fazendo

. Para que não exista nehuma solução real, ou seja, a reta não intersecione o gráfico, basta tomar
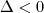
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Claudin » Sex Jun 15, 2012 02:40
por Claudin » Sex Jun 15, 2012 02:40
Valeu pela dica Russman.

Irei refazer o exercício e amanha posto se consegui ou se continuo com alguma dúvida.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Parábola]Determinar vértice de parábola (Urgente!)
por migvas99 » Seg Out 08, 2012 14:37
- 1 Respostas
- 2861 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 17:09
Funções
-
- [Parábola] Encontrando o ponto na parábola
por Ana_Rodrigues » Ter Nov 22, 2011 20:44
- 1 Respostas
- 5010 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 21:38
Geometria Analítica
-
- Parábola
por flavio2010 » Sáb Jul 17, 2010 19:11
- 1 Respostas
- 2032 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 22:20
Funções
-
- Parábola
por flavio2010 » Dom Jul 18, 2010 19:42
- 1 Respostas
- 1925 Exibições
- Última mensagem por Tom

Dom Jul 18, 2010 23:31
Funções
-
- Parábola
por flavio2010 » Sex Jul 23, 2010 19:16
- 1 Respostas
- 2023 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 24, 2010 01:40
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
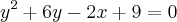 , determine os valores de
, determine os valores de  para que a reta
para que a reta 

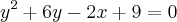 , determine os valores de
, determine os valores de  para que a reta
para que a reta 

, determine os valores de
para que a reta

 na equação.
na equação. 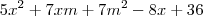

na equação.
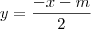 , você deveria obter:
, você deveria obter: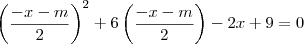
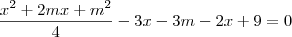
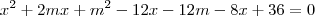
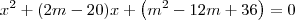
 . Em seguida, use a análise que lhe foi explicada em seu outro tópico.
. Em seguida, use a análise que lhe foi explicada em seu outro tópico.

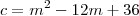 .
. e
e 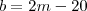 .
. da equação é
da equação é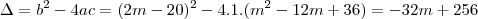 .
. isto é garantido. Já, para a reta ser tangente deve existir apenas um ponto de intersecção que é garantido fazendo
isto é garantido. Já, para a reta ser tangente deve existir apenas um ponto de intersecção que é garantido fazendo  . Para que não exista nehuma solução real, ou seja, a reta não intersecione o gráfico, basta tomar
. Para que não exista nehuma solução real, ou seja, a reta não intersecione o gráfico, basta tomar 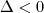 .
.

