ola, estou tentando resolver essa questão, eu obtenho a resposta 0,3 porem a resposta correta é 0,33.
Uma urna A contém duas bolas brancas e três bolas pretas. Uma urna B tem uma bola branca e duas pretas. Uma bola é transferida ao acaso, da urna A para a urna B. Em seguida uma bola é transferida ao acaso, da urna B para a urna A. Extraem-se, então, duas bolas ao acaso, da urna A. Calcular a probabilidade de que sejam duas bolas pretas.
Seja p(E) a probabilidade de um evento E:
Urna A no inicio: 5 bolas em total =>
p(bola branca) = 2/5, p(bola preta) = 3/5.
Urna B no inicio: 3 bolas em total =>
p(bola branca) = 1/3, p(bola preta) = 2/3.
Urna A após a 1a transferência:
p(sacar bola branca) = 2/5, p(sacar bola preta) = 3/5.
Urna B após a 1a transferência:
p(agregar bola branca) = 2/5, p(agregar bola preta) = 3/5 =>
p(2 bola brancas) = 2/5, p(3 bola pretas) = 3/5.
Urna B após a 2a transferência:
p((sacar bola branca) de (duas brancas e duas pretas)) = 2/4 x 2/5
p((sacar bola preta) de (duas brancas e duas pretas)) = 2/4 x 2/5
p((sacar bola branca) de (uma brancas e três pretas)) = 1/4 x 3/5
p((sacar bola preta) de (uma brancas e três pretas)) = 3/4 x 3/5
Urna A após a 2a transferência:
p((agregar bola branca) de (duas brancas e duas pretas da B)) = 2/4 x 2/5
p((agregar bola preta) de (duas brancas e duas pretas)) = 2/4 x 2/5
p((agregar bola branca) de (uma brancas e três pretas da B)) = 1/4 x 3/5
p((agregar bola preta) de (uma brancas e três pretas)) = 3/4 x 3/5
dai ja tentei de tdo


 uma probabilidade i qualquer, (UA) a urna A, (UB) a urna B, B as bolas Brancas e de P as bolas Pretas.
uma probabilidade i qualquer, (UA) a urna A, (UB) a urna B, B as bolas Brancas e de P as bolas Pretas.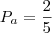

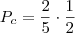



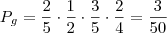
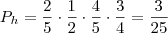



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.