 por iceman » Seg Mai 28, 2012 19:52
por iceman » Seg Mai 28, 2012 19:52
Determine o conjugado do número complexo

Não consigo resolver, ajuda aí?
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Seg Mai 28, 2012 20:57
por Russman » Seg Mai 28, 2012 20:57
É so trocar i por -i.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por iceman » Seg Mai 28, 2012 21:06
por iceman » Seg Mai 28, 2012 21:06
Russman escreveu:É so trocar i por -i.
Mas qual é o calculo? não sei fazer. Ajuda?
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por joaofonseca » Qua Mai 30, 2012 15:54
por joaofonseca » Qua Mai 30, 2012 15:54
Russman escreveu:É so trocar i por -i.
Não me parece!Primeiro é necessário colocar

na forma

.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Molina » Qua Mai 30, 2012 16:16
por Molina » Qua Mai 30, 2012 16:16
Boa tarde.
O que Russman quis dizer é que
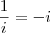
Tente agora...

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Russman » Qua Mai 30, 2012 16:36
por Russman » Qua Mai 30, 2012 16:36
Molina escreveu:Boa tarde.
O que Russman quis dizer é que
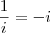
Tente agora...

Sim, escreve o número na forma normal e onde aparece

troca-se por

.
Veja que, colocando

na forma Normal, isto é

, temos
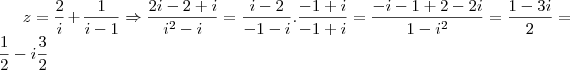
.
Portanto o conjugado é
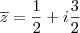
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por joaofonseca » Qua Mai 30, 2012 17:15
por joaofonseca » Qua Mai 30, 2012 17:15
Parece que houve um erro nesses calculos, antes da multiplicação pelo conjugado do denominador
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Complexos- demonstração com conjugado.
por emsbp » Sex Ago 03, 2012 18:10
- 2 Respostas
- 1864 Exibições
- Última mensagem por emsbp

Sex Ago 03, 2012 19:17
Números Complexos
-
- conjugado e simétrico
por anamendes » Sáb Mai 19, 2012 07:54
- 1 Respostas
- 1700 Exibições
- Última mensagem por emsbp

Sex Ago 03, 2012 18:21
Números Complexos
-
- Limites, conjugado de raizes
por moyses » Qui Out 06, 2011 12:16
- 19 Respostas
- 25744 Exibições
- Última mensagem por LuizAquino

Dom Out 09, 2011 19:16
Cálculo: Limites, Derivadas e Integrais
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17114 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- complexos
por irineu junior » Dom Mar 14, 2010 15:41
- 1 Respostas
- 1945 Exibições
- Última mensagem por DanielFerreira

Seg Mar 15, 2010 04:31
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 na forma
na forma  .
.
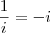


 troca-se por
troca-se por  .
. na forma Normal, isto é
na forma Normal, isto é  , temos
, temos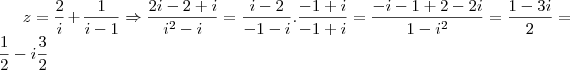 .
.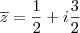



 .
.
 :
: