Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite - como resolver um lim quando temos raiz^2 e raiz^3.
por Monica santos » Sex Ago 16, 2013 14:22
- 4 Respostas
- 4192 Exibições
- Última mensagem por young_jedi
Sex Ago 16, 2013 19:01
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo: limite com raiz dentro de raiz
por roberto_trebor » Sáb Fev 15, 2014 20:45
- 1 Respostas
- 2267 Exibições
- Última mensagem por Man Utd
Dom Fev 16, 2014 17:58
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] raiz
por beel » Ter Set 06, 2011 13:48
- 5 Respostas
- 2671 Exibições
- Última mensagem por beel
Sex Set 09, 2011 16:52
Cálculo: Limites, Derivadas e Integrais
-
- Limite com Raiz
por mayconf » Sex Set 28, 2012 14:54
- 5 Respostas
- 3476 Exibições
- Última mensagem por gabriel feron
Dom Set 30, 2012 20:07
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE]raiz/ duvida
por beel » Dom Set 11, 2011 15:09
- 6 Respostas
- 2989 Exibições
- Última mensagem por beel
Dom Out 16, 2011 16:59
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25
Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.
Caso ainda não tenha dado uma
, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
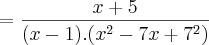
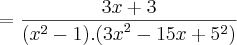
![\lim_{x\rightarrow1}\frac{\sqrt[3]{x+7} -2}{x-1}](/latexrender/pictures/e86db2c9295317d306248de599c57da4.png "\lim_{x\rightarrow1}\frac{\sqrt[3]{x+7} -2}{x-1}")
![\lim_{x\rightarrow1}\frac{\sqrt[3]{x+7} -2}{x-1}.\frac{({x}^{2}-7x+{7}^{2})}{({x}^{2}-7x+{7}^{2})}](/latexrender/pictures/a4a95694dc57888d3e1e042aade9d9ee.png "\lim_{x\rightarrow1}\frac{\sqrt[3]{x+7} -2}{x-1}.\frac{({x}^{2}-7x+{7}^{2})}{({x}^{2}-7x+{7}^{2})}")
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5} -2}{{x}^{2}-1}](/latexrender/pictures/81b708725d2bedff7be8967ab9e3313d.png "\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5} -2}{{x}^{2}-1}")
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5} -2}{{x}^{2}-1}.\frac{({3x}^{2}-15x+{5}^{2})}{({3x}^{2}-15x+{5}^{2})}](/latexrender/pictures/61abfbf370479bc3c636b6ba4494d71a.png "\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5} -2}{{x}^{2}-1}.\frac{({3x}^{2}-15x+{5}^{2})}{({3x}^{2}-15x+{5}^{2})}")
por Thyago Quimica » Sex Mai 25, 2012 18:08 
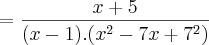
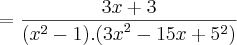
![\lim_{x\rightarrow 1} \frac{\sqrt[3]{x+7}-2}{x-1}](/latexrender/pictures/41d7e9c95eced925669b27b2bca3edbb.png "\lim_{x\rightarrow 1} \frac{\sqrt[3]{x+7}-2}{x-1}")
![\lim_{x\rightarrow 1} \frac{\sqrt[3]{x+7}-2}{x-1} .\frac{\sqrt[3]{(x+7)^2}+2.\sqrt[3]{x+7}+4}{\sqrt[3]{(x+7)^2}+2.\sqrt[3]{x+7}+4}](/latexrender/pictures/0cbbdaaedeef16a46370a972dd0504a1.png "\lim_{x\rightarrow 1} \frac{\sqrt[3]{x+7}-2}{x-1} .\frac{\sqrt[3]{(x+7)^2}+2.\sqrt[3]{x+7}+4}{\sqrt[3]{(x+7)^2}+2.\sqrt[3]{x+7}+4}")
![\lim_{x\rightarrow 1} \frac{x+7-8}{(x-1)(\sqrt[3]{(x+7)^2}+2.\sqrt[3]{x+7}+4)}](/latexrender/pictures/39d0058ad899f32e858fbd8811be2350.png "\lim_{x\rightarrow 1} \frac{x+7-8}{(x-1)(\sqrt[3]{(x+7)^2}+2.\sqrt[3]{x+7}+4)}")
![\lim_{x\rightarrow 1} \frac{1}{\sqrt[3]{(x+7)^2}+2.\sqrt[3]{x+7}+4} = \frac{1}{12}](/latexrender/pictures/863f07301566f0abf528745d965dd25d.png "\lim_{x\rightarrow 1} \frac{1}{\sqrt[3]{(x+7)^2}+2.\sqrt[3]{x+7}+4} = \frac{1}{12}")
