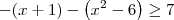haiashi escreveu:dados f(x)= -|x² - 6|+7 e g(x) = |x+1| eu estou tentando encontrar ;
1- as coordenadas dos pontos de interseção entre os dois gráficos f(x) e g(x)
2- quais são os intervalos onde f(x) =< g(x).
haiashi escreveu:na "1" eu tentei igualar f(x) = g(x)
-|x² - 6|+7 = |x + 1|
|x + 1| + |x² - 6| = 7
daí eu fico em divergencia, não sei como proceder pra resolver essas duas questoes para que eu possa fazer o grafico. alguém poderia me ajudar?
Aplicando a definição de módulo, temos que:

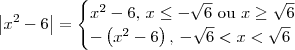
Sendo assim, a equação
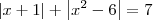
divide-se em quatro.
Equação 1) Para
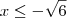
.
 Equação 2)
Equação 2) Para
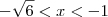
.
 Equação 3)
Equação 3) Para
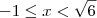
.
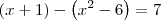 Equação 4)
Equação 4) Para
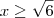
.
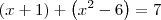
Resolvendo essas equações você pode determinar os pontos de interseção. Mas lembre-se que em cada equação o valor de x encontrado deve respeitar o intervalo no qual a equação está definida.
Em relação ao item 2), note que a inequação

pode ser arrumada como
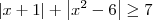
. Sendo assim, aplicando novamente a definição de módulo temos que essa inequação divide-se em quatro.
Inequação 1) Para
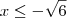
.
 Inequação 2)
Inequação 2) Para
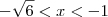
.
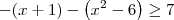 Inequação 3)
Inequação 3) Para
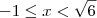
.
 Inequação 4)
Inequação 4) Para
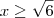
.

Resolvendo essas inequações você pode determinar os intervalos nos quais

. Mas lembre-se que a solução de cada inequação deve estar contida no intervalo no qual a inequação está definida.
Agora tente concluir o exercício.



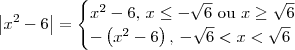
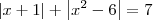 divide-se em quatro.
divide-se em quatro.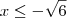 .
.
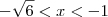 .
.
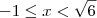 .
.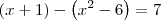
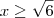 .
.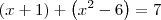
 pode ser arrumada como
pode ser arrumada como 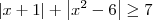 . Sendo assim, aplicando novamente a definição de módulo temos que essa inequação divide-se em quatro.
. Sendo assim, aplicando novamente a definição de módulo temos que essa inequação divide-se em quatro.