Pessoal estou tentando a tempos e não consigo resolver este exercícios de G.A, alguém poderia me ajudar?
Exercício: Determine a equação hiperbole de vértices A1=(1,-2), A2=(5, -2), sabendo que um dos focos é F=(6,-2).
Agradeço.



gustavohenrique escreveu:Pessoal estou tentando a tempos e não consigo resolver este exercícios de G.A, alguém poderia me ajudar?
Exercício: Determine a equação hiperbole de vértices A1=(1,-2), A2=(5, -2), sabendo que um dos focos é F=(6,-2).
Agradeço.
 ====> a = 2
====> a = 2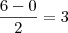 ====> c = 3
====> c = 3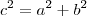 ====>
====> 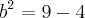 ====>
====> 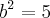





Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
