To com 2 questões que tão me encucando aqui.
1-(Puccamp) - O desmatamento no estado do Acre está avançando a uma taxa constante de 16 campos de futebol por hora.Num dado instante, a área devastada equivale a 261 760 campos de futebol.Sabendo-se que as dimensões médias de um campo de futebol são : 95m por 68 m, ao fim de 360 dias, o total de área devastada, em quilômetros quadrados será:
O que fiz: Área de um campo = 6 460
6460*14 (campos por hora) = 90 440
90440 * 24 (h de 1 dia)= 2 170 560
ou seja, em 1 dia, são devastados 2 170 560 metros
2 170 560*360 = metros devastados em 360 dias, que dá um número absurdamente grande, ou seja, não sei resolver essa questão
2 - Ufpe - Seja f(n) =
, onde n é um número inteiro . Analise as afirmativas a seguir( )F(n) é um número inteiro qualquer que seja n
( )f(n) maior que 0 se n maior que 1.
( )Existe n tal que f(n) é um número racional não inteiro.
( )Se m é menor que n então f(m) é menor que f(n)
( ) F(n) é menor que n para todo n.
Se dessem uma explicação a cada afirmativa seria show,
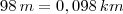e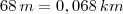 
. Equivalentemente, pegue o resultado que você encontrou e multiplique por 
para determinar o valor em kilometros quadrados.
e efetue a divisão. Avalie cada afirmação a partir disso.
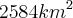
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.