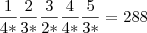"(UCSAL) O enunciado abaixo refere-se às questões de número 09 e 10.
Um jogo é formado por 52 fichas, divididas em quatro grupos de cores distintas - vermelha, azul, verde e amarela - e, em cada grupo, as fichas são enumeradas de 1 a 13.
09. De quantos modos pode-se distribuir aleatoriamente um grupo de 5 fichas a um jogador, sendo que três delas estejam marcadas com o número 8 e as demais com números iguais?
a)48 b)96 c)192 d)288 e)570
10. A probabilidade de um jogador receber aleatoriamente 4 fichas, sendo duas verdes e duas amarelas, é?"
O gabarito diz que na questão 09 dá letra 'd', 288 e na 10 dá