 por Lorrane12 » Qui Abr 26, 2012 15:22
por Lorrane12 » Qui Abr 26, 2012 15:22
Na figura, ABCD é um quadrado e CF = AG = 2 . Calcule CE
- Anexos
-
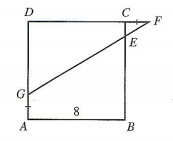
- Imagem do quadrado
- cats.jpg (5.84 KiB) Exibido 3178 vezes
-
Lorrane12
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mar 23, 2012 19:36
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por nakagumahissao » Seg Abr 30, 2012 00:08
por nakagumahissao » Seg Abr 30, 2012 00:08
Você não colocou neste fórum o que já tentou fazer para resolver o problema, no entanto, eis a solução:

Olhando no diagrama modificado acima, você poderá utilizar as relações dos triângulos e suas proporções para resolver o problema, ou seja: (Temos 8 + 2 em um dos lados do triângulo maior que se relaciona com om 2 do triângulo menor)


Portanto,

Creio que esta resposta satisfaz a o problema exposto.
Editado pela última vez por
nakagumahissao em Ter Mai 01, 2012 01:03, em um total de 1 vez.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por DanielFerreira » Ter Mai 01, 2012 00:31
por DanielFerreira » Ter Mai 01, 2012 00:31
Nakagumahissao,
como concluiu que CD = 8 e DG = 6?
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por nakagumahissao » Ter Mai 01, 2012 01:00
por nakagumahissao » Ter Mai 01, 2012 01:00
No seu problema, em sua figura, consta 8 em AB, assim, como estamos lidando com um quadrado, consequentemente, CD =8. Para se chegar a DG = 6, note que se todos os lados do quadrado são iguais e valem 8, DG + GA = 8 => DG = 8 - GA => DG = 8 - 2 => DG = 6;
Espero ter respondido suas perguntas convenientemente.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por DanielFerreira » Ter Mai 01, 2012 01:08
por DanielFerreira » Ter Mai 01, 2012 01:08
nakagumahissao escreveu:No seu problema, em sua figura, consta 8 em AB, assim, como estamos lidando com um quadrado, consequentemente, CD =8. Para se chegar a DG = 6, note que se todos os lados do quadrado são iguais e valem 8, DG + GA = 8 => DG = 8 - GA => DG = 8 - 2 => DG = 6;
Espero ter respondido suas perguntas convenientemente.
E aí meu camarada, blz?
Não postei esse problema, apenas indaguei esses valores por não ter conseguido visualizá-los. Quando o copiei para uma folha, equivocadamente, não vi esse 8.
Por isso não consegui concluir nada! Rsrsr
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por nakagumahissao » Ter Mai 01, 2012 01:27
por nakagumahissao » Ter Mai 01, 2012 01:27
Sem problema. Nem notei também que era você escrevendo ao invés da pessoa que postou originalmente o problema. Vlw
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ache x na figura em questão
por Balanar » Dom Out 17, 2010 14:31
- 2 Respostas
- 1599 Exibições
- Última mensagem por Balanar

Dom Out 17, 2010 15:32
Geometria Plana
-
- como calcular o volume da figura
 por eliane e rodrigo » Seg Ago 23, 2010 22:33
por eliane e rodrigo » Seg Ago 23, 2010 22:33
- 2 Respostas
- 2098 Exibições
- Última mensagem por eliane e rodrigo

Ter Ago 24, 2010 16:45
Geometria Espacial
-
- [energia mecânica] Figura desenhada ...
por gustavoluiss » Ter Set 06, 2011 00:01
- 1 Respostas
- 2068 Exibições
- Última mensagem por Neperiano

Ter Set 06, 2011 14:53
Álgebra Elementar
-
- Qual o radiano formado na figura abaixo
 por andersontricordiano » Seg Jun 06, 2011 15:14
por andersontricordiano » Seg Jun 06, 2011 15:14
- 1 Respostas
- 4137 Exibições
- Última mensagem por DanielFerreira

Seg Jun 06, 2011 18:00
Geometria
-
- Derivada - calcular a area da figura rotacionada
por maykonnunes » Qui Set 15, 2011 23:54
- 4 Respostas
- 3707 Exibições
- Última mensagem por LuizAquino

Sáb Set 24, 2011 00:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.












