A área do paralelogramo que pode ser formado por dois vetores

e

é dada pelo módulo se seu produto vetorial, isto é, seja S a área entao
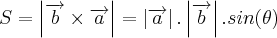
,
onde

é o angulo entre os vetores.
Efetuando o produto vetorial observamos que


,
pois

e
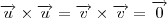
.
Portanto,

Para confirmar isto podemos calcular de outra forma. Pois bem, o problema pede que você calcule a área do paralelogramo entre os vetores

e

. Assim, você precisa conhecer o módulo destes vetores e o angulo entre eles! ( Veja que a soma e a subtração de veotres geram novos vetores).
É conhecido e facilmente demons trável que
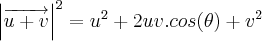
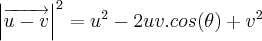
,
onde as letras sem flechas representam o módulo do respectivo vetor, isto é,

e

o angulo ja mencionado.
Assim,
![{\left|\overrightarrow{u+v} \right|}^{2} = {u}^{2} + 2uv.cos(\theta) + {v}^{2} = {6}^{2} + 2.6.4.cos({30}^{o}) + {4}^{2} = 52 + 24\sqrt[]{3} {\left|\overrightarrow{u+v} \right|}^{2} = {u}^{2} + 2uv.cos(\theta) + {v}^{2} = {6}^{2} + 2.6.4.cos({30}^{o}) + {4}^{2} = 52 + 24\sqrt[]{3}](/latexrender/pictures/23d9f8d54d83bb0e1e26d27a4072762b.png)
.
![{\left|\overrightarrow{u+v} \right|}^{2} = {u}^{2} + 2uv.cos(\theta) + {v}^{2} = {6}^{2} - 2.6.4.cos({30}^{o}) + {4}^{2} = 52 - 24\sqrt[]{3} {\left|\overrightarrow{u+v} \right|}^{2} = {u}^{2} + 2uv.cos(\theta) + {v}^{2} = {6}^{2} - 2.6.4.cos({30}^{o}) + {4}^{2} = 52 - 24\sqrt[]{3}](/latexrender/pictures/275f1cf9134d7eef267cfa8aacebc128.png)
.
Agora, o angulo entres estes veotores podemos calcular usando o produto escalar.
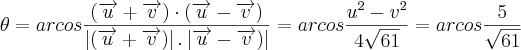
De onde,
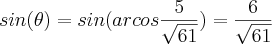
. Portanto,

.
O primeiro método é bem mais simples e direto.


 e
e  é dada pelo módulo se seu produto vetorial, isto é, seja S a área entao
é dada pelo módulo se seu produto vetorial, isto é, seja S a área entao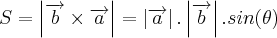 ,
, é o angulo entre os vetores.
é o angulo entre os vetores.
 ,
, e
e 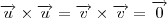 .
.
 e
e  . Assim, você precisa conhecer o módulo destes vetores e o angulo entre eles! ( Veja que a soma e a subtração de veotres geram novos vetores).
. Assim, você precisa conhecer o módulo destes vetores e o angulo entre eles! ( Veja que a soma e a subtração de veotres geram novos vetores).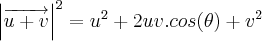
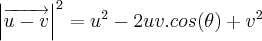 ,
, e
e ![{\left|\overrightarrow{u+v} \right|}^{2} = {u}^{2} + 2uv.cos(\theta) + {v}^{2} = {6}^{2} + 2.6.4.cos({30}^{o}) + {4}^{2} = 52 + 24\sqrt[]{3} {\left|\overrightarrow{u+v} \right|}^{2} = {u}^{2} + 2uv.cos(\theta) + {v}^{2} = {6}^{2} + 2.6.4.cos({30}^{o}) + {4}^{2} = 52 + 24\sqrt[]{3}](/latexrender/pictures/23d9f8d54d83bb0e1e26d27a4072762b.png) .
.![{\left|\overrightarrow{u+v} \right|}^{2} = {u}^{2} + 2uv.cos(\theta) + {v}^{2} = {6}^{2} - 2.6.4.cos({30}^{o}) + {4}^{2} = 52 - 24\sqrt[]{3} {\left|\overrightarrow{u+v} \right|}^{2} = {u}^{2} + 2uv.cos(\theta) + {v}^{2} = {6}^{2} - 2.6.4.cos({30}^{o}) + {4}^{2} = 52 - 24\sqrt[]{3}](/latexrender/pictures/275f1cf9134d7eef267cfa8aacebc128.png) .
.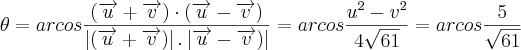
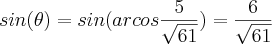 . Portanto,
. Portanto, .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.