 por Suellen » Qui Abr 12, 2012 22:50
por Suellen » Qui Abr 12, 2012 22:50
Primeiramente, boa noite.
Sou nova aqui no fórum e gosto de resolver exercícios, pena que não são todos que consigo completar.
(já consegui resolver varios tipos desses exercicios, mas por não colocar em prática não me lembro mais)

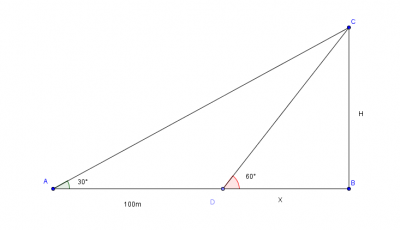
-Uma pessoa vê o topo de uma torre sob um ângulo de 30º. Caminhando 100m em linha reta, aproximando-se da torre, alcança um segundo ponto, de onde vê o topo sob um ângulo de 60º. Qual a distância da torre ao segundo ponto?
(OBS:queria mostrar juntamente uma figura do exercicio, mas não sei ainda como ponho aqui, o que faço?)
-
Suellen
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 12, 2012 22:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Edu-sjc » Sex Abr 13, 2012 13:09
por Edu-sjc » Sex Abr 13, 2012 13:09
Se esta for a figura eu fiz assim.
No triâgulo ABC temos que:
![tg30°=\frac{H}{100+x} \Rightarrow H=\left(100+x \right)\frac{\sqrt[2]{3}}{2} tg30°=\frac{H}{100+x} \Rightarrow H=\left(100+x \right)\frac{\sqrt[2]{3}}{2}](/latexrender/pictures/4e9aafafece82c42492be7a4a7a2882c.png)
E no triâgulo BCD temos que:
![tg60°=\frac{H}{x} \Rightarrow x\sqrt[2]{3}=H tg60°=\frac{H}{x} \Rightarrow x\sqrt[2]{3}=H](/latexrender/pictures/555ba9d2252db272622cb4bfdda37b01.png)
Agora só igualar o H, teremos:
![x\sqrt[2]{3}=\left(100+x \right)\frac{\sqrt[2]{3}}{2} \Rightarrow 2x=100+x \Rightarrow x=100m x\sqrt[2]{3}=\left(100+x \right)\frac{\sqrt[2]{3}}{2} \Rightarrow 2x=100+x \Rightarrow x=100m](/latexrender/pictures/879a275ed3defc7b40b7833934edcbbc.png)
Espero que esta seja a resposta. E para colocar a imagem é só você vir em adicionar um anexo, clicar em selecionar um arquivo e abrir a imagem salvo no seu computador, blz

espero ter ajudado!!!
- Anexos
-
-
Edu-sjc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Out 26, 2011 12:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Suellen » Seg Abr 16, 2012 19:12
por Suellen » Seg Abr 16, 2012 19:12
obg. acho que entendi.
até mais..
-
Suellen
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 12, 2012 22:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Ter Mai 01, 2012 00:42
por DanielFerreira » Ter Mai 01, 2012 00:42
Edu,
vc cometeu um equívoco no valor de tg 30°.
![tg 30^0 = \frac{\sqrt[]{3}}{3} tg 30^0 = \frac{\sqrt[]{3}}{3}](/latexrender/pictures/6ae685ec7cca2d2f2b6e440273f7a18b.png)
Edu-sjc escreveu:Se esta for a figura eu fiz assim.
No triâgulo ABC temos que:
![tg30^0=\frac{H}{100+x} \Rightarrow H=\left(100+x \right)\frac{\sqrt[]{3}}{3} tg30^0=\frac{H}{100+x} \Rightarrow H=\left(100+x \right)\frac{\sqrt[]{3}}{3}](/latexrender/pictures/669fe86319b1cc54aa31b6f488a9e6c2.png)
E no triâgulo BCD temos que:
![tg60^0=\frac{H}{x} \Rightarrow x\sqrt[]{3}=H tg60^0=\frac{H}{x} \Rightarrow x\sqrt[]{3}=H](/latexrender/pictures/5391617bb0c865a29ea15e41c70b544b.png)
Agora só igualar o H, teremos:
![x\sqrt[]{3}=\left(100+x \right)\frac{\sqrt[]{3}}{3} \Rightarrow 3x=100+x \Rightarrow x=50m x\sqrt[]{3}=\left(100+x \right)\frac{\sqrt[]{3}}{3} \Rightarrow 3x=100+x \Rightarrow x=50m](/latexrender/pictures/d18cddead868f80b82a57bd4bf1f2f02.png)
Espero que esta seja a resposta. E para colocar a imagem é só você vir em adicionar um anexo, clicar em selecionar um arquivo e abrir a imagem salvo no seu computador, blz

espero ter ajudado!!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Suellen » Qui Mai 03, 2012 17:57
por Suellen » Qui Mai 03, 2012 17:57
é verdade "dan".
obg pela correção.
-
Suellen
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 12, 2012 22:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qui Mai 03, 2012 20:53
por DanielFerreira » Qui Mai 03, 2012 20:53
Não há de quê!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Edu-sjc » Seg Mai 07, 2012 10:42
por Edu-sjc » Seg Mai 07, 2012 10:42
Poh que mancada!!
-
Edu-sjc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Out 26, 2011 12:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculos envolvendo triângulo retângulo e retângulo
 por andersontricordiano » Seg Abr 18, 2011 02:29
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 4031 Exibições
- Última mensagem por MarceloFantini

Seg Abr 18, 2011 04:19
Progressões
-
- Triangulo Retangulo
por ginrj » Qui Jun 04, 2009 18:56
- 1 Respostas
- 3408 Exibições
- Última mensagem por ginrj

Seg Jun 15, 2009 18:14
Geometria Plana
-
- Triângulo retângulo
por DanielFerreira » Qua Jul 29, 2009 15:38
- 5 Respostas
- 6822 Exibições
- Última mensagem por Cleyson007

Qui Jul 30, 2009 17:22
Trigonometria
-
- Triângulo retangulo
por cristina » Seg Set 21, 2009 14:56
- 3 Respostas
- 2203 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 14:18
Trigonometria
-
- Triângulo retângulo
por DanielFerreira » Qui Mar 03, 2011 11:26
- 1 Respostas
- 2121 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 14:43
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![tg30°=\frac{H}{100+x} \Rightarrow H=\left(100+x \right)\frac{\sqrt[2]{3}}{2} tg30°=\frac{H}{100+x} \Rightarrow H=\left(100+x \right)\frac{\sqrt[2]{3}}{2}](/latexrender/pictures/4e9aafafece82c42492be7a4a7a2882c.png)
![tg60°=\frac{H}{x} \Rightarrow x\sqrt[2]{3}=H tg60°=\frac{H}{x} \Rightarrow x\sqrt[2]{3}=H](/latexrender/pictures/555ba9d2252db272622cb4bfdda37b01.png)
![x\sqrt[2]{3}=\left(100+x \right)\frac{\sqrt[2]{3}}{2} \Rightarrow 2x=100+x \Rightarrow x=100m x\sqrt[2]{3}=\left(100+x \right)\frac{\sqrt[2]{3}}{2} \Rightarrow 2x=100+x \Rightarrow x=100m](/latexrender/pictures/879a275ed3defc7b40b7833934edcbbc.png)
 espero ter ajudado!!!
espero ter ajudado!!!![tg 30^0 = \frac{\sqrt[]{3}}{3} tg 30^0 = \frac{\sqrt[]{3}}{3}](/latexrender/pictures/6ae685ec7cca2d2f2b6e440273f7a18b.png)
![tg30^0=\frac{H}{100+x} \Rightarrow H=\left(100+x \right)\frac{\sqrt[]{3}}{3} tg30^0=\frac{H}{100+x} \Rightarrow H=\left(100+x \right)\frac{\sqrt[]{3}}{3}](/latexrender/pictures/669fe86319b1cc54aa31b6f488a9e6c2.png)
![tg60^0=\frac{H}{x} \Rightarrow x\sqrt[]{3}=H tg60^0=\frac{H}{x} \Rightarrow x\sqrt[]{3}=H](/latexrender/pictures/5391617bb0c865a29ea15e41c70b544b.png)
![x\sqrt[]{3}=\left(100+x \right)\frac{\sqrt[]{3}}{3} \Rightarrow 3x=100+x \Rightarrow x=50m x\sqrt[]{3}=\left(100+x \right)\frac{\sqrt[]{3}}{3} \Rightarrow 3x=100+x \Rightarrow x=50m](/latexrender/pictures/d18cddead868f80b82a57bd4bf1f2f02.png)

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.