Boa noite a todos, gostaria de uma ajuda em um limite:
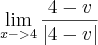
tenho a resolução do problema, porém não consegui entender o porque de dar -1 o resultado. Não consigo concordar com o (-).
Obrigada!

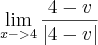

Luisags escreveu:Olá!
Boa noite a todos, gostaria de uma ajuda em um limite:
tenho a resolução do problema, porém não consegui entender o porque de dar -1 o resultado. Não consigo concordar com o (-).
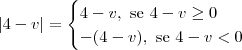
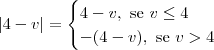
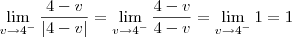
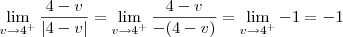
 .
.



gabriel feron escreveu:se a questao nao estivesse com modulo:
o que aconteceria? o que mudaria em relacao a com modulo

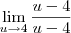






Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes

 .
.



