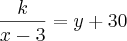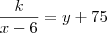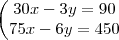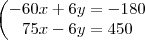por JUNIOR FELIX » Dom Abr 15, 2012 00:06
por JUNIOR FELIX » Dom Abr 15, 2012 00:06
UM CASAL FOI COMPRAR UMA GELADEIRA EM X PRESTAÇÕES IGUAIS. COMPRANDO A GELADEIRA COM TRÊS PRESTAÇÕES A MENOS, CADA PRESTAÇÃO AUMENTARIA R$30,00, E SE COMPRASSE COM 6 PRESTAÇÕES A MENOS, CADA PRESTAÇÃO AUMENTARIA R$75,00. O CASAL DECIDIU ENTÃO COMPRAR A GELADEIRA PAGANDO EM X PRESTAÇÕES. NESSAS CONDIÇÕES O VALOR DE X É:
a) 30
b) 24
c) 18
d) 15
e) 12
tentei inicialmente pensar em igualar a incógnita
x-3=p+30
x-6= p+75
multiplicando a 1ª equação por -2 e transformando em sistema teriamos:
-2x+6=-2p-60
x-6= p+75
igual a -x=-p+15 então substituindo x=p-15 em
x-6=p+75 temos p-15=p+75 que é igual a 2p=90 temos que p=45 não seiiiiii
-
JUNIOR FELIX
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Abr 14, 2012 23:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: RH
- Andamento: formado
 por DanielFerreira » Sáb Abr 21, 2012 14:29
por DanielFerreira » Sáb Abr 21, 2012 14:29
Valor da geladeira ==========> k
valor de cada prestação =====> y
quantidade de prestações ===> x
Temos então:
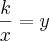
===========>
k = xyOu seja, ao dividirmos o valor da geladeira pelas suas parcelas iguais teremos o valor de cada uma - que são iguais!
Com esse raciocínio, desenvolveremos outras duas equações, veja:
(...)COMPRANDO A GELADEIRA COM TRÊS PRESTAÇÕES A MENOS, CADA PRESTAÇÃO AUMENTARIA R$30,00,(...)
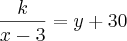
xy + 30x - 3y - 90 = k
30x - 3y - 90 = k - xy
30x - 3y - 90 = 0
30x - 3y = 90E SE COMPRASSE COM 6 PRESTAÇÕES A MENOS, CADA PRESTAÇÃO AUMENTARIA R$75,00.
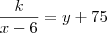
xy + 75x - 6y - 450 = k
75x - 6y - 450 = k - xy
75x - 6y - 450 = 0
75x - 6y = 450 Resolvendo as equações em
negrito:
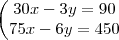
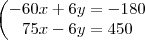
----------------------------
75x - 60x = 450 - 180
15x = 270
x = 18"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação do 1º Grau - Como montar a equação
por macedo1967 » Sáb Out 07, 2017 12:53
- 1 Respostas
- 8029 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:17
Equações
-
- [Equação Modular] com equação de 2º grau
por paola-carneiro » Qui Abr 05, 2012 15:53
- 2 Respostas
- 3407 Exibições
- Última mensagem por paola-carneiro

Sex Abr 06, 2012 16:23
Funções
-
- Equação do 1 Grau
por luanxd » Ter Jan 26, 2010 00:06
- 3 Respostas
- 5503 Exibições
- Última mensagem por Cleyson007

Qua Jan 27, 2010 20:40
Polinômios
-
- equação do 2º grau
por juniorthai » Seg Fev 08, 2010 12:05
- 2 Respostas
- 11745 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 06, 2010 20:48
Trigonometria
-
- equação do 2º grau
por juniorthai » Qui Fev 11, 2010 08:15
- 6 Respostas
- 8336 Exibições
- Última mensagem por lulopes

Sex Dez 08, 2017 20:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


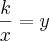 ===========>
===========>