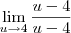por Luisags » Qui Abr 12, 2012 23:05
por Luisags » Qui Abr 12, 2012 23:05
Olá!
Boa noite a todos, gostaria de uma ajuda em um limite:
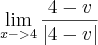
tenho a resolução do problema, porém não consegui entender o porque de dar -1 o resultado. Não consigo concordar com o (-).
Obrigada!
-
Luisags
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 12, 2012 22:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia química
- Andamento: cursando
 por LuizAquino » Qui Abr 12, 2012 23:48
por LuizAquino » Qui Abr 12, 2012 23:48
Luisags escreveu:Olá!
Boa noite a todos, gostaria de uma ajuda em um limite:
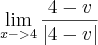
tenho a resolução do problema, porém não consegui entender o porque de dar -1 o resultado. Não consigo concordar com o (-).
Pela definição de módulo, temos que:
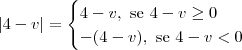
Ou seja, temos que:
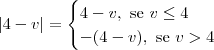
Calculando então esse limite, temos que:
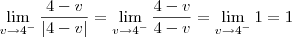
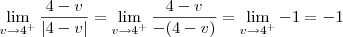
Como esses limites laterais são diferentes, temos que não existe o limite:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Luisags » Sex Abr 13, 2012 00:51
por Luisags » Sex Abr 13, 2012 00:51
Muito obrigada, LuizAquino!
Consegui entender o porque, agora.
Boa noite!
-
Luisags
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 12, 2012 22:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia química
- Andamento: cursando
 por gabriel feron » Seg Abr 16, 2012 03:55
por gabriel feron » Seg Abr 16, 2012 03:55
Desculpa retornar o assunto, mas sou iniciante no calculo 1, to correndo atras, dai queria tirar uma duvida
se a questao nao estivesse com modulo:

o que aconteceria? o que mudaria em relacao a com modulo
muito obrigado e desculpe qualquer inconveniência(primeira vez que estou usando o forum).
-
gabriel feron
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Abr 16, 2012 03:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Hídrica
- Andamento: cursando
 por LuizAquino » Seg Abr 16, 2012 15:34
por LuizAquino » Seg Abr 16, 2012 15:34
gabriel feron escreveu:se a questao nao estivesse com modulo:

o que aconteceria? o que mudaria em relacao a com modulo
O que você escreveu é equivalente a:

Mas o que você deseja é na verdade:
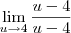
Nesse caso, você deveria ter escrito algo como:

Note a importância de colocar os parênteses.
Vamos agora analisar esse limite.
Suponha que você tenha um número real x (diferente de zero). Quanto vale x/x? Ora, isso vale 1.
No limite de seu exemplo, temos o número u - 4. Como u está se aproximando de 4, mas não é 4, temos que u - 4 é diferente de zero. Sendo assim, quanto vale (u - 4)/(u - 4) ? Ora, isso vale 1.
Temos então o seguinte:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por gabriel feron » Ter Abr 17, 2012 03:17
por gabriel feron » Ter Abr 17, 2012 03:17
Entendi, muito obrigado, na verdade eu sabia so que pela falta de atencao nao me liguei, to comecando o calculo agora ^^
obs: sobre o parentes eu achei que tinha corrigido, mas bom que agora ja aprendi a fazer limite pelo editor de formulas!

valeu!!!

-
gabriel feron
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Abr 16, 2012 03:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Hídrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dificuldade com limites em cálculo I
por Vidotti » Dom Nov 04, 2012 20:42
- 4 Respostas
- 2496 Exibições
- Última mensagem por Vidotti

Dom Nov 04, 2012 21:17
Cálculo: Limites, Derivadas e Integrais
-
- [limites] Dificuldade com raízes
por baloso » Sex Abr 25, 2014 19:22
- 2 Respostas
- 2046 Exibições
- Última mensagem por baloso

Seg Abr 28, 2014 19:33
Cálculo: Limites, Derivadas e Integrais
-
- Subtração de modulos, em uma inequação
por ferrazrafael » Qua Set 01, 2010 15:35
- 1 Respostas
- 3898 Exibições
- Última mensagem por MarceloFantini

Qua Set 01, 2010 20:52
Funções
-
- Inequações com soma de módulos
 por Caroline Oliveyra » Dom Jul 10, 2011 13:03
por Caroline Oliveyra » Dom Jul 10, 2011 13:03
- 9 Respostas
- 16462 Exibições
- Última mensagem por Caroline Oliveyra

Qua Jul 13, 2011 16:22
Sistemas de Equações
-
- resolver inequaçao com modulos
por rodrigonapoleao » Qua Dez 19, 2012 22:40
- 1 Respostas
- 1637 Exibições
- Última mensagem por e8group

Qui Dez 20, 2012 20:00
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
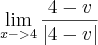

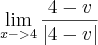

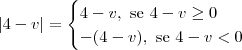
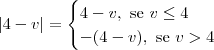
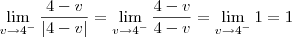
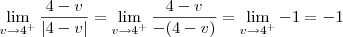
 .
.