Olá, estou vendo equação geometria anaitica.
Tenho dúvidas nesta questão:
Substitua a equação polar r=4tg0.sec0 pela equação cartesiana equivalente:
Para transformar de polar para cartesianas oque sei são estas formulas:
X=rcos0
Y=rsen0
Até agora não tinha resolvido nenhuma questão igual a esta onde possuo uma equação.
Como faço para resolver? Preciso de ajuda para clarear este exercicio:
Att


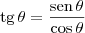
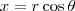 e
e  , temos que:
, temos que:
 na equação polar você pode substituir por
na equação polar você pode substituir por  .
. .
.

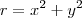 e sim
e sim 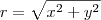 . Segundo,
. Segundo,  , use isso.
, use isso.

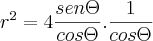

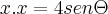
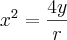

 ao quadrado sem elevar o segundo lado. Em todo caso, veja que o colega Luiz mostrou que
ao quadrado sem elevar o segundo lado. Em todo caso, veja que o colega Luiz mostrou que  . Analogamente, vemos que
. Analogamente, vemos que  .
.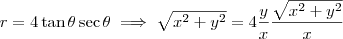 . Consegue continuar a partir daí?
. Consegue continuar a partir daí?
 .
.
 :
: