acalves escreveu:ok, então toda vez que no enunciado tiver com o menor número possível eu acho mdc com o maior número possível eu acho mmc,posso guardar assim?
obrigada.
Não. Esse raciocínio só funciona no caso de menor número possível, onde se usa o MDC. Não existe caso de maior número possível porque, não importa o comprimento dos lados do cubo que você escolher, sempre poderá ser reduzido.
Usa-se o MMC, por exemplo, em casos de periodicidade:
Três máquinas recebem manutenção. A primeira recebe manutenção de 3 em 3 dias, a segunda de 4 em quatro dias e a terceira de 5 em 5 dias. Se as máquinas recebem manutenção hoje, todas juntas, quantos dias levará para que elas recebam manutenção juntas ?
Nesse caso, a primeira recebe em dias múltiplos de 3 a segunda de 4 e a terceira em múltiplos de 5. Logo, um multiplo comum às máquinas é um dia em que as três recebem manutenção. Como o menor múltiplo é o próximo dia:
MMC(3,4,5) = 60
Daqui a 60 dias elas voltarão a receber manutenção juntas.



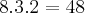 cubos
cubos
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)