Tô com uma dúvida cruel aqui. Na equação diferencial de Bernoulli, para linearizá-la tenho que fazer uma substituição do tipo:

Porém, preciso derivar para concluir a linearização. Na minha cabeça, a derivada disso é:

Mas a resposta ainda tem um
 sendo multiplicado, ou seja
sendo multiplicado, ou seja
Alguém poderia me explicar de onde vem esse
 ?
?Obrigado =)


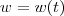 e
e  , ou seja, você tem duas funções que dependem de um outro parâmetro
, ou seja, você tem duas funções que dependem de um outro parâmetro  , sendo que a segunda você tem uma composição de
, sendo que a segunda você tem uma composição de  com
com  . Usando a regra da cadeia, você tem que
. Usando a regra da cadeia, você tem que 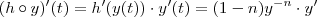 .
.


 .
.
 :
: