 por Arthur_Bulcao » Qua Mar 28, 2012 19:19
por Arthur_Bulcao » Qua Mar 28, 2012 19:19
Estou com problema ao calcular o limite:
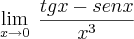
Não sei nem por onde começar.
Já estudei teorema dos confrontos.
Agradeço qualquer ajuda
-
Arthur_Bulcao
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Mar 23, 2012 17:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Graduação em Engenharia Acústica
- Andamento: cursando
 por fraol » Qua Mar 28, 2012 22:38
por fraol » Qua Mar 28, 2012 22:38
Se você aplicar o limite diretamente chegará a

que é um tipo de indeterminação.
Minha sugestão é você usar a Regra de L'Hopital. Essa regra diz que

onde f' e g' são, respectivamente, as derivadas do numerador e do denominador (há algumas restrições de aplicação, mas não é o caso aqui já que as funções são deriváveis nas proximidades de x = 0).
Se você optar por usar L'Hopital, deverá aplicar a regra sucessivamente até sair dos vários

que irão surgindo. Ao final, se tudo estiver ok você obterá

como resposta.
No caso de não conhecer a regra sugiro que você pesquise a respeito e, também, assista a aula sobre esse assunto do nosso colega de forum, o professor LuizAquino, que está no endereço
http://www.youtube.com/watch?v=-TNbOIad3Oc.
Agora, a título de curiosidade (minha

), pois essa função é um tanto complexa, fiz um gráfico no Geogebra e parte dele está abaixo. Veja que o valor da função aproxima-se de

para x aproximando-se de 0 por ambos os lados.

- funcao
- func-tanx-senx-sobre-x3.png (9.61 KiB) Exibido 1740 vezes
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por LuizAquino » Qua Mar 28, 2012 23:31
por LuizAquino » Qua Mar 28, 2012 23:31
Arthur_Bulcao escreveu:Estou com problema ao calcular o limite:
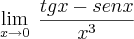
fraol escreveu:Se você aplicar o limite diretamente chegará a

que é um tipo de indeterminação.
Minha sugestão é você usar a Regra de L'Hopital. Essa regra diz que

Um caminho é usar a Regra de L'Hospital. Mas nesse caso não é necessário.
Aplicando a definição de tangente, temos que:






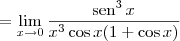
![= \left(\lim_{x\to 0} \dfrac{\textrm{sen}\, x}{x}\right)^3 \left[\lim_{x\to 0} \dfrac{1}{\cos x(1 + \cos x)}\right] = \left(\lim_{x\to 0} \dfrac{\textrm{sen}\, x}{x}\right)^3 \left[\lim_{x\to 0} \dfrac{1}{\cos x(1 + \cos x)}\right]](/latexrender/pictures/0742a984672207912df272076c22a2af.png)
Agora fica fácil concluir o exercício.
fraol escreveu:No caso de não conhecer a regra sugiro que você pesquise a respeito e, também, assista a aula sobre esse assunto do nosso colega de forum, o professor LuizAquino, que está no endereço
http://www.youtube.com/watch?v=-TNbOIad3Oc.
Obrigado por indicar a videoaula.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Arthur_Bulcao » Qui Mar 29, 2012 19:13
por Arthur_Bulcao » Qui Mar 29, 2012 19:13
Puxa, obrigado.
Eu só não uso L'Hospital, porque o professor ainda não deu derivadas, e não aceitaria numa prova, por enquanto.

-
Arthur_Bulcao
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Mar 23, 2012 17:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Graduação em Engenharia Acústica
- Andamento: cursando
 por LuizAquino » Qui Mar 29, 2012 23:23
por LuizAquino » Qui Mar 29, 2012 23:23
Arthur_Bulcao escreveu:Puxa, obrigado.
Eu só não uso L'Hospital, porque o professor ainda não deu derivadas, e não aceitaria numa prova, por enquanto.
A Regra de L'Hospital costuma deixar o estudante "preguiçoso". Ele acaba não aprendendo a efetuar simplificações algébricas, pois na Regra de L'Hospital basta aplicar algumas derivadas. Mas só que usualmente o conceito de derivadas só é estudado depois que já houve o estudo de limites! Em resumo: quando iniciamos o estudo de limites não podemos usar a Regra de L'Hospital. O ideal é deixar essa regra para calcular alguns limites específicos, que não possuem simplificação algébrica.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5409 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4755 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4783 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4809 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2794 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
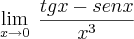

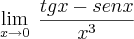

 que é um tipo de indeterminação.
que é um tipo de indeterminação.
 que irão surgindo. Ao final, se tudo estiver ok você obterá
que irão surgindo. Ao final, se tudo estiver ok você obterá  como resposta.
como resposta. para x aproximando-se de 0 por ambos os lados.
para x aproximando-se de 0 por ambos os lados.
que é um tipo de indeterminação.







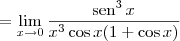
![= \left(\lim_{x\to 0} \dfrac{\textrm{sen}\, x}{x}\right)^3 \left[\lim_{x\to 0} \dfrac{1}{\cos x(1 + \cos x)}\right] = \left(\lim_{x\to 0} \dfrac{\textrm{sen}\, x}{x}\right)^3 \left[\lim_{x\to 0} \dfrac{1}{\cos x(1 + \cos x)}\right]](/latexrender/pictures/0742a984672207912df272076c22a2af.png)






 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.