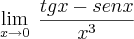
Não sei nem por onde começar.
Já estudei teorema dos confrontos.
Agradeço qualquer ajuda

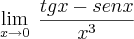

 que é um tipo de indeterminação.
que é um tipo de indeterminação.
 que irão surgindo. Ao final, se tudo estiver ok você obterá
que irão surgindo. Ao final, se tudo estiver ok você obterá  como resposta.
como resposta. para x aproximando-se de 0 por ambos os lados.
para x aproximando-se de 0 por ambos os lados.
Arthur_Bulcao escreveu:Estou com problema ao calcular o limite:
fraol escreveu:Se você aplicar o limite diretamente chegará aque é um tipo de indeterminação.
Minha sugestão é você usar a Regra de L'Hopital. Essa regra diz que






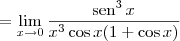
![= \left(\lim_{x\to 0} \dfrac{\textrm{sen}\, x}{x}\right)^3 \left[\lim_{x\to 0} \dfrac{1}{\cos x(1 + \cos x)}\right] = \left(\lim_{x\to 0} \dfrac{\textrm{sen}\, x}{x}\right)^3 \left[\lim_{x\to 0} \dfrac{1}{\cos x(1 + \cos x)}\right]](/latexrender/pictures/0742a984672207912df272076c22a2af.png)
fraol escreveu:No caso de não conhecer a regra sugiro que você pesquise a respeito e, também, assista a aula sobre esse assunto do nosso colega de forum, o professor LuizAquino, que está no endereço http://www.youtube.com/watch?v=-TNbOIad3Oc.

Um caminho é usar a Regra de L'Hospital. Mas nesse caso não é necessário.
Aplicando a definição de tangente, temos que:
Agora fica fácil concluir o exercício.


Arthur_Bulcao escreveu:Puxa, obrigado.
Eu só não uso L'Hospital, porque o professor ainda não deu derivadas, e não aceitaria numa prova, por enquanto.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

