 por Ana_Rodrigues » Seg Mar 26, 2012 19:05
por Ana_Rodrigues » Seg Mar 26, 2012 19:05
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fraol » Seg Mar 26, 2012 21:44
por fraol » Seg Mar 26, 2012 21:44
Eu fiz os cálculos e cheguei na mesma inversa que você.
Para tirar a dúvida quanto ao resultado, você pode multiplicar a matriz original pela inversa (tanto a sua como a do gabarito) . O resultado deve ser a matriz identidade (pois se a inversa existe, então

). Assim você terá certeza da resposta.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matriz Inversa
por Cleyson007 » Qui Ago 20, 2009 17:49
- 5 Respostas
- 4471 Exibições
- Última mensagem por Cleyson007

Sáb Ago 22, 2009 10:45
Matrizes e Determinantes
-
- Matriz - Inversa ou não?
por Bruhh » Seg Mar 08, 2010 16:31
- 7 Respostas
- 16108 Exibições
- Última mensagem por Neperiano

Qui Mar 11, 2010 15:50
Conversão de Unidades
-
- [Matriz Inversa]
por vanessafey » Seg Set 12, 2011 15:17
- 4 Respostas
- 3273 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 23:23
Matrizes e Determinantes
-
- Matriz Inversa
por Claudin » Qui Set 15, 2011 17:44
- 11 Respostas
- 5259 Exibições
- Última mensagem por MarceloFantini

Qui Set 15, 2011 18:51
Matrizes e Determinantes
-
- Inversa da Matriz
por brunojorge29 » Seg Out 10, 2011 09:48
- 4 Respostas
- 2903 Exibições
- Última mensagem por brunojorge29

Qua Out 12, 2011 17:30
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





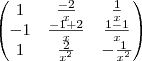





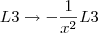

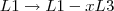
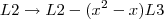
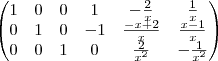
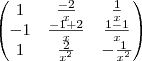

 ). Assim você terá certeza da resposta.
). Assim você terá certeza da resposta.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.