 por carolina camargo » Ter Jun 16, 2009 16:44
por carolina camargo » Ter Jun 16, 2009 16:44
Como tirar o MMC dessa função:
![\frac{2}{-k+\sqrt[]{k^2-144}}+\frac{2}{-k-\sqrt[]{k^2-144}}=\frac{5}{12} \frac{2}{-k+\sqrt[]{k^2-144}}+\frac{2}{-k-\sqrt[]{k^2-144}}=\frac{5}{12}](/latexrender/pictures/0a26fa73dca6296c427f1a108d450edb.png)
Ainda sou iniciante e tenho muita dificuldade.
Obrigada!
-
carolina camargo
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jun 16, 2009 16:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Cleyson007 » Ter Jun 16, 2009 19:02
por Cleyson007 » Ter Jun 16, 2009 19:02
Boa tarde Carolina!
Primeiramente, seja bem vinda ao Ajuda Matemática.
Carolina, você tem o gabarito da questão?
Quero ver se confirma com minha resposta

Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Qua Jun 17, 2009 10:22
por Cleyson007 » Qua Jun 17, 2009 10:22
Bom dia Carolina!
Vou apresentar como estou resolvendo:
MMC da equação:
![(-k+\sqrt[2]{{k}^{2}-144})(-k-\sqrt[2]{{k}^{2}-144}) (-k+\sqrt[2]{{k}^{2}-144})(-k-\sqrt[2]{{k}^{2}-144})](/latexrender/pictures/730c9edd6fb57f15e8f10e714b13c55a.png)
Sabendo o MMC fica fácil

(Basta dividir o MMC pelo denominador e multiplicar pelo numerador)
Resolvendo, encontra-se
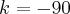
Qualquer dúvida é só informar.

Espero ter ajudado.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por carolina camargo » Qua Jun 17, 2009 16:08
por carolina camargo » Qua Jun 17, 2009 16:08
Cleyson, obrigada pela ajuda.
De acordo com meus cálculos deu k= -15
-
carolina camargo
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jun 16, 2009 16:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Cleyson007 » Qua Jun 17, 2009 18:21
por Cleyson007 » Qua Jun 17, 2009 18:21
carolina camargo escreveu:Cleyson, obrigada pela ajuda.
De acordo com meus cálculos deu k= -15
Olá Carolina!
Carolina, por favor apresente o seu modo de resolução... assim vamos descobrir onde está havendo divergência na resolução

Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Qua Jun 17, 2009 19:27
por Molina » Qua Jun 17, 2009 19:27
Cleyson007 escreveu:carolina camargo escreveu:Cleyson, obrigada pela ajuda.
De acordo com meus cálculos deu k= -15
Olá Carolina!
Carolina, por favor apresente o seu modo de resolução... assim vamos descobrir onde está havendo divergência na resolução

Até mais.
Um abraço.
Meu k também deu -15.
E acho que está correto, pois fiz a substituição e fechou!
Qualquer coisa joga isso daqui no google: (2/(15+sqrt(15^2 - 144)) + (2/(15-sqrt(15^2 - 144))
e isso daqui também: 5/12
Grande abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Qui Jun 18, 2009 08:38
por Cleyson007 » Qui Jun 18, 2009 08:38
Bom dia!
Já que está havendo uma divergência das respostas, vou explicar como resolvi:
O mmc encontrado foi:
![(-k+\sqrt[2]{{k}^{2}-144})(-k-\sqrt[2]{{k}^{2}-144}) (-k+\sqrt[2]{{k}^{2}-144})(-k-\sqrt[2]{{k}^{2}-144})](/latexrender/pictures/730c9edd6fb57f15e8f10e714b13c55a.png)
Resolvendo....
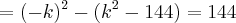
-2k+2\sqrt[2]({{k}^{2}-144)]}}}{144}=\frac{5}{2} \frac{[-2k-2\sqrt[2]({{k}^{2}-144)-2k+2\sqrt[2]({{k}^{2}-144)]}}}{144}=\frac{5}{2}](/latexrender/pictures/b33b7c58d7889b9478e198922f5427d8.png)

Logo,
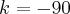 --> Talvez interpretei errado o exercício.... mas creio que a resolução está correta
--> Talvez interpretei errado o exercício.... mas creio que a resolução está correta 
Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por carolina camargo » Qui Jun 18, 2009 16:56
por carolina camargo » Qui Jun 18, 2009 16:56
Bom, não me dou muito bem com o "editor de fórmulas", mas acho que é isso.
![\frac{-4k}{\left(-k+\sqrt[]{k^2-144} \right)\left(-k-\sqrt[]{k^2-144} \right)}=\frac{5}{12}\Rightarrow \frac{-4k}{k^2-\left(k^2-144 \right)}=\frac{5}{12}
...
\Rightarrow \frac{-4k}{144}=\frac{5}{12}\Rightarrow -4k=\frac{720}{12}\Rightarrow k=\frac{60}{-4}\Rightarrow k=-15 \frac{-4k}{\left(-k+\sqrt[]{k^2-144} \right)\left(-k-\sqrt[]{k^2-144} \right)}=\frac{5}{12}\Rightarrow \frac{-4k}{k^2-\left(k^2-144 \right)}=\frac{5}{12}
...
\Rightarrow \frac{-4k}{144}=\frac{5}{12}\Rightarrow -4k=\frac{720}{12}\Rightarrow k=\frac{60}{-4}\Rightarrow k=-15](/latexrender/pictures/c27e7e37f3caa10c874ede19c045f188.png)
abraço!
-
carolina camargo
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jun 16, 2009 16:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Cleyson007 » Sáb Jun 20, 2009 01:54
por Cleyson007 » Sáb Jun 20, 2009 01:54
Boa noite Carolina!
Carolina, desculpe... sua resolução está correta

Estava calculando colocando o segundo membro da equação como

.

Depois que eu fui reparar que é

...
Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{2}{-k+\sqrt[]{k^2-144}}+\frac{2}{-k-\sqrt[]{k^2-144}}=\frac{5}{12} \frac{2}{-k+\sqrt[]{k^2-144}}+\frac{2}{-k-\sqrt[]{k^2-144}}=\frac{5}{12}](/latexrender/pictures/0a26fa73dca6296c427f1a108d450edb.png)

![\frac{2}{-k+\sqrt[]{k^2-144}}+\frac{2}{-k-\sqrt[]{k^2-144}}=\frac{5}{12} \frac{2}{-k+\sqrt[]{k^2-144}}+\frac{2}{-k-\sqrt[]{k^2-144}}=\frac{5}{12}](/latexrender/pictures/0a26fa73dca6296c427f1a108d450edb.png)



![(-k+\sqrt[2]{{k}^{2}-144})(-k-\sqrt[2]{{k}^{2}-144}) (-k+\sqrt[2]{{k}^{2}-144})(-k-\sqrt[2]{{k}^{2}-144})](/latexrender/pictures/730c9edd6fb57f15e8f10e714b13c55a.png)
 (Basta dividir o MMC pelo denominador e multiplicar pelo numerador)
(Basta dividir o MMC pelo denominador e multiplicar pelo numerador)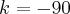








![(-k+\sqrt[2]{{k}^{2}-144})(-k-\sqrt[2]{{k}^{2}-144}) (-k+\sqrt[2]{{k}^{2}-144})(-k-\sqrt[2]{{k}^{2}-144})](/latexrender/pictures/730c9edd6fb57f15e8f10e714b13c55a.png)
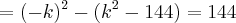
-2k+2\sqrt[2]({{k}^{2}-144)]}}}{144}=\frac{5}{2} \frac{[-2k-2\sqrt[2]({{k}^{2}-144)-2k+2\sqrt[2]({{k}^{2}-144)]}}}{144}=\frac{5}{2}](/latexrender/pictures/b33b7c58d7889b9478e198922f5427d8.png)

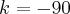


![\frac{-4k}{\left(-k+\sqrt[]{k^2-144} \right)\left(-k-\sqrt[]{k^2-144} \right)}=\frac{5}{12}\Rightarrow \frac{-4k}{k^2-\left(k^2-144 \right)}=\frac{5}{12}
...
\Rightarrow \frac{-4k}{144}=\frac{5}{12}\Rightarrow -4k=\frac{720}{12}\Rightarrow k=\frac{60}{-4}\Rightarrow k=-15 \frac{-4k}{\left(-k+\sqrt[]{k^2-144} \right)\left(-k-\sqrt[]{k^2-144} \right)}=\frac{5}{12}\Rightarrow \frac{-4k}{k^2-\left(k^2-144 \right)}=\frac{5}{12}
...
\Rightarrow \frac{-4k}{144}=\frac{5}{12}\Rightarrow -4k=\frac{720}{12}\Rightarrow k=\frac{60}{-4}\Rightarrow k=-15](/latexrender/pictures/c27e7e37f3caa10c874ede19c045f188.png)


 .
. 
 ...
...
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)