 por dina ribeiro » Sex Mar 23, 2012 21:03
por dina ribeiro » Sex Mar 23, 2012 21:03
Boa noite!!!
Resolvi a integral indeterminada abaixo mas quando olhei resolução do livro vi que final está diferente. Não consigo enxergar de onde saiu a última parte que diz que o resultado é 0. Não seria 1 ?!

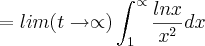
![=lim(t\rightarrow\propto) \left[-\frac{lnx}{x}-\frac{1}{x} \right] =lim(t\rightarrow\propto) \left[-\frac{lnx}{x}-\frac{1}{x} \right]](/latexrender/pictures/e24b1ba62754cfef59e56cadb8e75162.png)
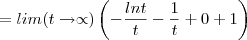

CONVERGE
Essa próxima parte não entendi:


CONVERGE
Grata
-
dina ribeiro
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 15, 2012 19:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Sex Mar 23, 2012 21:10
por MarceloFantini » Sex Mar 23, 2012 21:10
Dina, crie sempre novos tópicos para suas dúvidas. Isto ajuda a manter o fórum organizado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral - onde errei?
por dina ribeiro » Sex Mar 16, 2012 18:39
- 7 Respostas
- 3308 Exibições
- Última mensagem por dina ribeiro

Dom Mar 18, 2012 15:15
Cálculo: Limites, Derivadas e Integrais
-
- Onde foi que eu errei
por Gabriel Doria » Sex Mar 23, 2012 00:03
- 2 Respostas
- 1632 Exibições
- Última mensagem por MarceloFantini

Sex Mar 23, 2012 08:16
Cálculo: Limites, Derivadas e Integrais
-
- FATORIAL (ONDE EU ERREI?)
por natanskt » Qui Dez 02, 2010 17:33
- 3 Respostas
- 1949 Exibições
- Última mensagem por alexandre32100

Sex Dez 03, 2010 14:24
Binômio de Newton
-
- [Integral por partes] onde está o erro???
por Fabio Wanderley » Seg Mai 28, 2012 20:21
- 2 Respostas
- 2476 Exibições
- Última mensagem por Fabio Wanderley

Ter Mai 29, 2012 13:42
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Definida] Ex. do tipo "onde está o erro?"
por Fabio Wanderley » Seg Out 22, 2012 23:15
- 2 Respostas
- 2836 Exibições
- Última mensagem por Fabio Wanderley

Ter Out 23, 2012 00:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

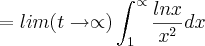
![=lim(t\rightarrow\propto) \left[-\frac{lnx}{x}-\frac{1}{x} \right] =lim(t\rightarrow\propto) \left[-\frac{lnx}{x}-\frac{1}{x} \right]](/latexrender/pictures/e24b1ba62754cfef59e56cadb8e75162.png)
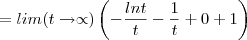
 CONVERGE
CONVERGE
 CONVERGE
CONVERGE




 .
.



