 por nakagumahissao » Ter Mai 01, 2012 01:16
por nakagumahissao » Ter Mai 01, 2012 01:16
Sendo t em Meses, o valor de t = 77,18 meses, ou seja:
Para sabermos quantos anos possuem 77,18 meses, dividimos por 12 meses, que representa um ano. Assim:
77,18 / 12 = 6,43166666, ou seja, 6 Anos. Retirando-se o 6 do número 6,4316666..., teremos:
6,431666... - 6 = 0,43166666 Anos (Menos de 1 ano)
Para sabermos quantos meses este valor representa, multiplicamos este resultado por 12 (1 ano possui 12 Meses). Desta forma:
0,4316666 x 12 = 5,1799992, ou seja, 5 Meses. Subtraindo-se 5 de 5,1799992, teremos:
5,1799992 - 5 = 0,1799992 Meses. De forma análoga, desta vez, para se saber a quantidade de dias em 0,1799992 meses, multiplicamos por 30 (média de dias em 1 mês), que finalmente, nos dará:
0,1799992 Meses x 30 = 5,399976 dias, o que equivale a aproximadamente 5 dias. O restante, 0,399976 foi ignorado.
Concluindo: 6 anos, 5 meses e 5 dias aproximadamente.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali



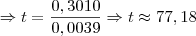



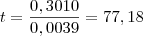

 .
.
 :
: