 por LuizCarlos » Sex Mar 16, 2012 18:49
por LuizCarlos » Sex Mar 16, 2012 18:49
Olá amigos!
Seguinte, estou fazendo exercícios, não estou entendendo essa questão:
Escreva a representação decimal de um número irracional compreendido entre 5 e 6 e de outro compreendido entre 3,1 e 3,2.
Como faço para encontrar números compreendidos entre dois números inteiros, e dois números decimais, no caso 3,1 e 3,2.
Abraço.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por MarceloFantini » Sex Mar 16, 2012 22:27
por MarceloFantini » Sex Mar 16, 2012 22:27
Primeiro, é bom perceber que não existe representação decimal finita de um número irracional, apenas as aproximações por racionais que tem, uma vez que pela
definição sabemos que um número racional é a divisão por dois números inteiros. Para esclarecer esse exercício, pense num número cuja raíz quadrada por exemplo esteja entre 5 e 6. Ou seja,

. Isto significa que, elevado ao quadrado, teremos
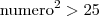
e

pois respeita a desigualdade. Daí, basta escolher algum que te interesse. Por exemplo,

.
Para facilitar o entendimento, usei "número", mas formalmente escreva alguma letra para denotar álgebra. Perdão pela falta de acento, não tem como no LaTeX.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Numero irracional entre numeros racionais
por Roni Martins » Qua Fev 24, 2010 10:36
- 1 Respostas
- 11874 Exibições
- Última mensagem por Molina

Qua Fev 24, 2010 13:18
Números Complexos
-
- [Equação irracional] Questão da EPCAR
por -daniel15asv » Sex Ago 03, 2012 17:16
- 3 Respostas
- 3596 Exibições
- Última mensagem por DanielFerreira

Sex Ago 17, 2012 21:40
Equações
-
- [Questão] Numero primo
por iuggui » Ter Mai 29, 2018 20:42
- 1 Respostas
- 2732 Exibições
- Última mensagem por DanielFerreira

Qui Mai 31, 2018 11:46
Aritmética
-
- Questão de Concurso-Número Complexos
por Pri Ferreira » Qua Mar 21, 2012 13:44
- 1 Respostas
- 1580 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 15:31
Números Complexos
-
- [módulo número complexo] Ajuda questao
por filipetrr » Qui Jun 27, 2013 10:43
- 5 Respostas
- 7288 Exibições
- Última mensagem por adauto martins

Qui Jan 08, 2015 11:28
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Isto significa que, elevado ao quadrado, teremos
. Isto significa que, elevado ao quadrado, teremos 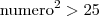 e
e  pois respeita a desigualdade. Daí, basta escolher algum que te interesse. Por exemplo,
pois respeita a desigualdade. Daí, basta escolher algum que te interesse. Por exemplo,  .
.
