 por ViniRFB » Dom Mar 11, 2012 17:18
por ViniRFB » Dom Mar 11, 2012 17:18
(FUVEST-2ª FASE) Os números x, raiz(x), log2 (10x) são, nessa ordem, os três primeiros termos de uma progressão geométrica. Calcule:
a) o 1º termo x.
b) o 5º termo.
Alguém me explica a parte abaixo transcrita?
O termo central é igual a média geométrica dos outros termos equidistantes a ele. Consequentemente, o quadrado do termo central é igual ao produto de dois termos equidistantes a ele.
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Dom Mar 11, 2012 21:25
por fraol » Dom Mar 11, 2012 21:25
ViniRFB escreveu:Alguém me explica a parte abaixo transcrita?
O termo central é igual a média geométrica dos outros termos equidistantes a ele. Consequentemente, o quadrado do termo central é igual ao produto de dois termos equidistantes a ele.
Suponha que
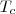
seja o termo central,
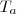
e

os termos equidistantes do termo central. Assim:
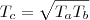
( a média geométrica ) , então
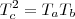
.
Por exemplo, na PG de razão 2: 1, 2, 4, 8, 16, 32, ... vamos escolher ao acaso 8 como termo central, repare que 2 e 32 são termos equidistantes, então

e
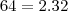
.
É isso.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por ViniRFB » Dom Mar 11, 2012 23:54
por ViniRFB » Dom Mar 11, 2012 23:54
Não entendi na verdade, mas verei com mais calma.
De todo modo obrigado.
ViniRFB
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Seg Mar 12, 2012 09:58
por fraol » Seg Mar 12, 2012 09:58
Ok. Se ao verificar quiser discutir algum ponto, manda pra cá.
Obrigado.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Seg Mar 12, 2012 17:10
por MarceloFantini » Seg Mar 12, 2012 17:10
Suponha que

e

estão em progressão geométrica. Então

, daí

. Entende a afirmação?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Seg Mar 12, 2012 17:20
por ViniRFB » Seg Mar 12, 2012 17:20
Sim.
A relação dela qual será então?
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Seg Mar 12, 2012 19:28
por MarceloFantini » Seg Mar 12, 2012 19:28
Note que no caso escolhi três termos consecutivos, o termo central é

. Note que na afirmação está embutido a noção de que existe um número
ímpar de termos, caso contrário não há termo central.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Seg Mar 12, 2012 22:51
por ViniRFB » Seg Mar 12, 2012 22:51
MarceloFantini escreveu:Note que no caso escolhi três termos consecutivos, o termo central é

. Note que na afirmação está embutido a noção de que existe um número
ímpar de termos, caso contrário não há termo central.
Bah Fantini.
Entendi. Muito obrigado mais uma vez pela excelente explicação e pelo empenho em fazer eu aprender o assunto.
Abração.
ViniRFB
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


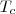 seja o termo central,
seja o termo central, 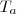 e
e  os termos equidistantes do termo central. Assim:
os termos equidistantes do termo central. Assim: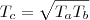 ( a média geométrica ) , então
( a média geométrica ) , então 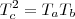 .
. e
e 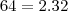 .
.
 e
e  estão em progressão geométrica. Então
estão em progressão geométrica. Então  , daí
, daí  . Entende a afirmação?
. Entende a afirmação?

 . Note que na afirmação está embutido a noção de que existe um número
. Note que na afirmação está embutido a noção de que existe um número