(FUVEST-2ª FASE) Os números x, raiz(x), log2 (10x) são, nessa ordem, os três primeiros termos de uma progressão geométrica. Calcule:
a) o 1º termo x.
b) o 5º termo.
Alguém me explica a parte abaixo transcrita?
O termo central é igual a média geométrica dos outros termos equidistantes a ele. Consequentemente, o quadrado do termo central é igual ao produto de dois termos equidistantes a ele.


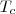 seja o termo central,
seja o termo central, 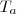 e
e  os termos equidistantes do termo central. Assim:
os termos equidistantes do termo central. Assim: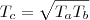 ( a média geométrica ) , então
( a média geométrica ) , então 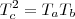 .
. e
e 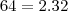 .
.
 e
e  estão em progressão geométrica. Então
estão em progressão geométrica. Então  , daí
, daí  . Entende a afirmação?
. Entende a afirmação?

 . Note que na afirmação está embutido a noção de que existe um número
. Note que na afirmação está embutido a noção de que existe um número ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)