alfabeta escreveu:Sejam A (1, 0) e B (5, 4?3) dois vértices de um triângulo equilátero ABC.
O vértice C está no 2°quadrante. Encontre-o.
Distancia entre:
(1, 0) (5, 4?3)
separação de dois pontos = ?((x? - x?)² + (y? - y?)²)
d = ?((1 - 5)² + (0 - 4?3)²)
d = ?((-4)² + (-4?3)²)
d = ?(16 + 48)
d = ?64
d = 8
Cheguei neste sistema:
(x - 1)² + y² = 64 e (x - 5)² + (y - 4?3)² = 64
Como resolver?
alfabeta escreveu:Eu fiz exatamente isto,mas cheguei no sistema de segundo grau e não sei resolver.
Note que tanto

quanto
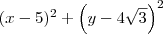
são iguais a 64. Desse modo, temos que:

Desenvolvendo essa equação, você obtém no final que:
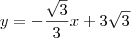
Agora escolha uma das equações e substitua y por
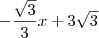
.
Dessa forma, você terá uma equação com apenas a incógnita x. Resolvendo essa equação, você obtém o valor de x.
Em seguida, basta usar o fato de que
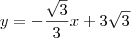
para determinar o valor de y.


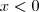 e
e 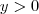 . Como ABC é equilátero, teremos
. Como ABC é equilátero, teremos  , ou seja, as distâncias de A até B, A até C e B até C são iguais entre si. Use isto.
, ou seja, as distâncias de A até B, A até C e B até C são iguais entre si. Use isto.

 quanto
quanto 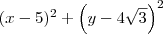 são iguais a 64. Desse modo, temos que:
são iguais a 64. Desse modo, temos que:
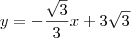
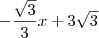 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

