 por ViniRFB » Sex Mar 02, 2012 13:39
por ViniRFB » Sex Mar 02, 2012 13:39
Amigos.
Preciso de um help nessa questão
57. (Analista Administrativo – ANEEL 2006/ESAF) Os números A,B e 10 formam,nessa ordem, uma progressão aritmética. Os números 1, A e B formam, nessa ordem,uma progressão geométrica. Com essas informações, pode-se afirmar que um possível valor para o produto das razões dessas progressões é igual a:
Gabarito - 12
Minha dúvida está na verdade na PG.
Na resolução dessa questão na PG está assim (1,A,B)
q= A/1 E q=B/A simplificando deu B= A²
QUERIA SABER COMO ISSO? SERIA APLICADO O MMC NA BASE? ALGUÉM PODERIA FAZER O PASSO A PASSO DESSA SIMPLIFICAÇÃO.
DESDE JÁ AGRADEÇO!
VINIRFB
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Sex Mar 02, 2012 13:44
por ViniRFB » Sex Mar 02, 2012 13:44
Pelo que deu para entender foi multiplicado em x as igualdades?
A/1=B/A Multiplicando em x fica A² e B resultando B=A², mas poderia fazer isso por quê?
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Sex Mar 02, 2012 19:00
por MarceloFantini » Sex Mar 02, 2012 19:00
Temos

. Logo,
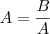
. Multiplique os dois lados por A, e lembre que
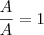
, daí
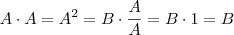
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Sex Mar 02, 2012 19:16
por ViniRFB » Sex Mar 02, 2012 19:16
Olá,
Não sei se entendi, mas acredito que ainda não, mas vamos lá...
A/1 = A correto? O resultado é A, pois toda letra dividade por um é a letra isso?
A = q é a razão da PG?
Do outro lado temos B/A. Essa parte eu não saquei eu acho. B/A é = B. A/A por que esse A/A novamente? Aí paira minha dúvida.
Grato
ViniRFB
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Sex Mar 02, 2012 21:57
por DanielFerreira » Sex Mar 02, 2012 21:57
ViniRFB escreveu:Amigos.
Preciso de um help nessa questão
57. (Analista Administrativo – ANEEL 2006/ESAF) Os números A,B e 10 formam,nessa ordem, uma progressão aritmética. Os números 1, A e B formam, nessa ordem,uma progressão geométrica. Com essas informações, pode-se afirmar que um possível valor para o produto das razões dessas progressões é igual a:
Gabarito - 12
Minha dúvida está na verdade na PG.
Na resolução dessa questão na PG está assim (1,A,B)
q= A/1 E q=B/A simplificando deu B= A²
QUERIA SABER COMO ISSO? SERIA APLICADO O MMC NA BASE? ALGUÉM PODERIA FAZER O PASSO A PASSO DESSA SIMPLIFICAÇÃO.
DESDE JÁ AGRADEÇO!
VINIRFB
P.A:




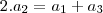
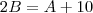
 P.G:
P.G:



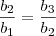
======>
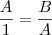
======>


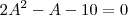
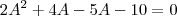
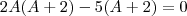

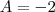
ou

Quando A = - 2, B = 4
r = B - A
r = 4 - (- 2)
r = 6

q = A
q = - 2
Então,
r . q =
6 . (- 2) =
- 12"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MarceloFantini » Sex Mar 02, 2012 23:00
por MarceloFantini » Sex Mar 02, 2012 23:00
Sim,

é a razão da progressão geométrica. Assim, para manter a razão, devemos ter que
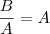
. Isto só acontece se

, para cancelar a divisão e sobrar

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Sex Mar 02, 2012 23:37
por ViniRFB » Sex Mar 02, 2012 23:37
Obrigado a todos pelas excelentes explicações.
ViniRFB
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4251 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4724 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25545 Exibições
- Última mensagem por Ananda

Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4234 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2888 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Logo,
. Logo, 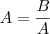 . Multiplique os dois lados por A, e lembre que
. Multiplique os dois lados por A, e lembre que 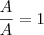 , daí
, daí 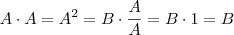 .
.






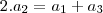
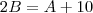





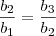 ======>
======> 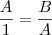 ======>
======> 

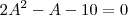
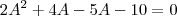
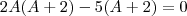

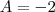 ou
ou 


 é a razão da progressão geométrica. Assim, para manter a razão, devemos ter que
é a razão da progressão geométrica. Assim, para manter a razão, devemos ter que 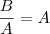 . Isto só acontece se
. Isto só acontece se  , para cancelar a divisão e sobrar
, para cancelar a divisão e sobrar 

 , avisa que eu resolvo.
, avisa que eu resolvo.

