Se f(x)=a^x, pode-se afirmar que f(x+1)-f(x-1) / f(2)-1 e igual a?
N entendi o significado de a elevado x? Obrigado por contribuir na minha preparacao!
por bmachado » Qua Fev 29, 2012 00:33
por LuizAquino » Qua Fev 29, 2012 12:24
bmachado escreveu:Se f(x)=a^x, pode-se afirmar que f(x+1)-f(x-1) / f(2)-1 e igual a?
bmachado escreveu:N entendi o significado de a elevado x? Obrigado por contribuir na minha preparacao!
.
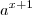.bmachado escreveu:f(x+1)-f(x-1) / f(2)-1
por bmachado » Qua Fev 29, 2012 16:51
LuizAquino escreveu:bmachado escreveu:Se f(x)=a^x, pode-se afirmar que f(x+1)-f(x-1) / f(2)-1 e igual a?bmachado escreveu:N entendi o significado de a elevado x? Obrigado por contribuir na minha preparacao!
É simplesmente uma função exponencial.
Por exemplo, onde há f(x+1) você irá substituir por
Onde há f(x-1) você irá substituir por
Por fim, onde há f(2) você irá substituir por
Com essas substituições, toda a expressão ficará dependente de a. A ideia do exercício é que você simplifique essa expressão ao máximo possível.
Agora eu aproveito para fazer uma observação.
Você escreveu a seguinte expressão no texto do exercício:bmachado escreveu:f(x+1)-f(x-1) / f(2)-1
Do jeito que está escrito, isso é o mesmo que:
Mas por acaso a expressão original no exercício seria como segue abaixo?
Se essa for a expressão correta, então você deveria ter escrito algo como:
(f(x+1)-f(x-1))/(f(2)-1)
Note o quanto é importante usar os parênteses de forma adequada!
Além disso, vale lembrar que para digitar as notações Matemáticas aqui no fórum você pode usar o LaTeX. Por favor, leia o tópico abaixo:
DICA: Escrevendo Fórmulas com LaTeX via BBCode
viewtopic.php?f=9&t=74
por Louis » Seg Jul 09, 2012 23:56
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
