 por Cleyson007 » Ter Fev 28, 2012 17:36
por Cleyson007 » Ter Fev 28, 2012 17:36
Boa tarde!
Calcule
![\int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]dx \int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]dx](/latexrender/pictures/796e820b7b113741419913f2cebf2a53.png)
Gabarito:

Se alguém puder ajudar, agradeço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizAquino » Ter Fev 28, 2012 17:56
por LuizAquino » Ter Fev 28, 2012 17:56
Cleyson007 escreveu:Calcule
![\int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]dx \int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]dx](/latexrender/pictures/796e820b7b113741419913f2cebf2a53.png)
Gabarito:

O que você já tentou fazer?
Você tem dúvida em algum ponto específico do cálculo dessa integral?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Cleyson007 » Ter Fev 28, 2012 18:14
por Cleyson007 » Ter Fev 28, 2012 18:14
Boa tarde Luiz Aquino!
Resolvi mas não encontrei a mesma resposta que o gabarito apresenta como correto.
Não postei minha resolução porque não consegui fazer no LateX o intervalo ao resolver a parte interna da integral (segunda integral).
Seria mais ou menos isso --> |3
Pode me ajudar?
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizAquino » Ter Fev 28, 2012 18:47
por LuizAquino » Ter Fev 28, 2012 18:47
Cleyson007 escreveu:Resolvi mas não encontrei a mesma resposta que o gabarito apresenta como correto.
Eis a primeira parte da resolução:
![\int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]\,dx = \int_{0}^{2}\left[{x}^{2}\frac{y^2}{2}\right]_1^3 \,dx \int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]\,dx = \int_{0}^{2}\left[{x}^{2}\frac{y^2}{2}\right]_1^3 \,dx](/latexrender/pictures/a8ad3e60e28ef89c432f39fa0aeff0d5.png)
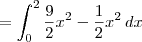
Agora tente finalizar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Cleyson007 » Qui Mar 01, 2012 16:12
por Cleyson007 » Qui Mar 01, 2012 16:12
Boa tarde Luiz Aquino!
Luiz, na primeira parte estamos derivando em função de y, correto? Se derivamos em função de y, o x é constante, não é mesmo?
Em meu ponto de vista seria:
![\left[{x}^{2}y\frac{{y}^{2}}{2} \right]\Leftrightarrow\left[\frac{{x}^{2}{y}^{3}}{2} \right] \left[{x}^{2}y\frac{{y}^{2}}{2} \right]\Leftrightarrow\left[\frac{{x}^{2}{y}^{3}}{2} \right]](/latexrender/pictures/66cacf41107f8f13f238060da19a8881.png)
Por que não pode ser escrito da forma que escrevi acima?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizAquino » Qui Mar 01, 2012 16:27
por LuizAquino » Qui Mar 01, 2012 16:27
Cleyson007 escreveu:Luiz, na primeira parte estamos derivando em função de y, correto? Se derivamos em função de y, o x é constante, não é mesmo?
Sim, correto.
Cleyson007 escreveu:Em meu ponto de vista seria:
![\left[{x}^{2}y\frac{{y}^{2}}{2} \right]\Leftrightarrow\left[\frac{{x}^{2}{y}^{3}}{2} \right] \left[{x}^{2}y\frac{{y}^{2}}{2} \right]\Leftrightarrow\left[\frac{{x}^{2}{y}^{3}}{2} \right]](/latexrender/pictures/66cacf41107f8f13f238060da19a8881.png)
Por que não pode ser escrito da forma que escrevi acima?
Se
c é uma constante, quanto vale a integral abaixo?
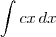
Ora, sabemos que:
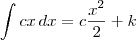
Sendo assim, lembrando que a constante agora é
x² ao invés de
c, quanto seria a integral abaixo?

Ora, ela seria:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Dúvida com uma integral simples
por Leonardo Ribeiro » Sex Abr 03, 2015 20:02
- 1 Respostas
- 2080 Exibições
- Última mensagem por Leonardo Ribeiro

Sex Abr 03, 2015 21:06
Cálculo: Limites, Derivadas e Integrais
-
- [integral] duvida integral
por lucasdemirand » Ter Nov 26, 2013 17:47
- 0 Respostas
- 903 Exibições
- Última mensagem por lucasdemirand

Ter Nov 26, 2013 17:47
Cálculo: Limites, Derivadas e Integrais
-
- Duvida na Integral
por rodrigo ff » Sex Mar 23, 2012 17:44
- 1 Respostas
- 1531 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 19:01
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] - Dúvida
por digsydinner » Ter Mar 27, 2012 10:37
- 3 Respostas
- 1863 Exibições
- Última mensagem por LuizAquino

Sex Mar 30, 2012 00:07
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em Integral
por Cleyson007 » Qua Abr 18, 2012 16:35
- 1 Respostas
- 909 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 14:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]dx \int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]dx](/latexrender/pictures/796e820b7b113741419913f2cebf2a53.png)


![\int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]dx \int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]dx](/latexrender/pictures/796e820b7b113741419913f2cebf2a53.png)




![\int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]\,dx = \int_{0}^{2}\left[{x}^{2}\frac{y^2}{2}\right]_1^3 \,dx \int_{0}^{2}\left[\int_{1}^{3}{x}^{2}y\,dy \right]\,dx = \int_{0}^{2}\left[{x}^{2}\frac{y^2}{2}\right]_1^3 \,dx](/latexrender/pictures/a8ad3e60e28ef89c432f39fa0aeff0d5.png)
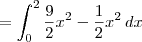

![\left[{x}^{2}y\frac{{y}^{2}}{2} \right]\Leftrightarrow\left[\frac{{x}^{2}{y}^{3}}{2} \right] \left[{x}^{2}y\frac{{y}^{2}}{2} \right]\Leftrightarrow\left[\frac{{x}^{2}{y}^{3}}{2} \right]](/latexrender/pictures/66cacf41107f8f13f238060da19a8881.png)

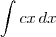
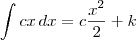



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.