Como resolver essa questão da Ufpel?

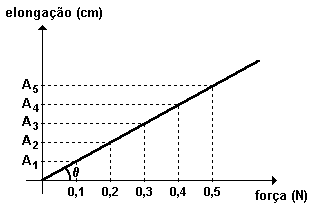
[ativirginis]

(Ufpel 2000) Observando-se a variação da elongação A (acréscimo de comprimento em cm) de uma mola, em função de uma força F (em N) aplicada sobre a mola, obtiveram-se os resultados que podem ser representados pela função linear abaixo:



Nessas condições, se š = arc tan 5, pode-se afirmar que cada aumento de 0,25N na força corresponde a um aumento na elongação de

a) 0,50 cm.

b) 2,00 cm.

c) 1,25 cm.

d) 3,75 cm.

e) 2,25 cm.

[LuizAquino]

(Ufpel 2000) Observando-se a variação da elongação A (acréscimo de comprimento em cm) de uma mola, em função de uma força F (em N) aplicada sobre a mola, obtiveram-se os resultados que podem ser representados pela função linear abaixo:

grafico.png (1.69 KiB) Exibido 4965 vezes

Nessas condições, se s = arc tan 5, pode-se afirmar que cada aumento de 0,25N na força corresponde a um aumento na elongação de

a) 0,50 cm.

b) 2,00 cm.

c) 1,25 cm.

d) 3,75 cm.

e) 2,25 cm.

Eu presumo que no texto original do exercício, ao invés de , há na verdade .

Dito isso, vejamos a resolução.

Sabemos que uma reta pode representar o gráfico de uma função polinomial do primeiro grau.

Sabemos ainda que essa função tem o formato f(x) = ax + b, sendo que a é chamado de coeficiente angular e b é chamado de coeficiente linear.

Sabemos que o coeficiente angular corresponde a tangente do ângulo formado entre a reta e o eixo x.

No caso da reta representada na figura, esse ângulo é .

Como no exercício diz que , temos que .

Sendo assim, já sabemos que o coeficiente angular é 5. Ou seja, a função tem o formato f(x) = 5x + b.

Além disso, observando a figura percebemos que a reta passa pelo ponto (0, 0). Ou seja, temos que f(0)=0. Sendo assim, 5*0 + b = 0. Isso significa que b = 0.

Em resumo: a função é f(x)=5x.

A questão pergunta qual é o aumento da elongação caso a força aumente em 0,25 N.

Vamos supor que a força fosse k. Se ela aumentou 0,25 N, então ela passou a ser k + 0,25.

A elongação para x = k será f(k). Ou seja, será 5k.

Já a elongação para x = k + 0,25 será f(k+0,25). Ou seja, será 5(k+0,25).

Dessa forma, a elongação passou de 5k para 5(k+0,25).

Ou seja, o seu aumento (em cm) foi de:
5(k+0,25) - 5k =
= 5k + 1,25 - 5k
= 1,25

Observação

Em uma função polinomial do primeiro grau, dada por f(x) = ax + b, quando a variável x aumenta c unidades, a variável y aumenta ac unidades.

Se a pessoa já souber essa informação, então esse exercício fica direto.

Como foi dado que , deduzimos que o coeficiente angular é 5. Isto é, a = 5.

Portanto, como a variável x aumentou 0,25 N, a variável y irá aumentar 5*0,25 = 1,25 cm.